
【題目】設(shè)函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的極值;
的極值;
(2)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)若對任意![]() 及任意
及任意![]() ,恒有
,恒有![]() 成立,求實數(shù)m的取值范圍.
成立,求實數(shù)m的取值范圍.
【答案】(1)極小值為1,無極大值;(2)詳見解析;(3)![]() .
.
【解析】
(1)當(dāng)![]() 時,求得函數(shù)的導(dǎo)數(shù),求得函數(shù)的單調(diào)性,進(jìn)而求得函數(shù)的極值;
時,求得函數(shù)的導(dǎo)數(shù),求得函數(shù)的單調(diào)性,進(jìn)而求得函數(shù)的極值;
(2)![]() 時,求得函數(shù)導(dǎo)數(shù)
時,求得函數(shù)導(dǎo)數(shù)![]() ,分類討論,即可求得函數(shù)的單調(diào)性,得到答案;
,分類討論,即可求得函數(shù)的單調(diào)性,得到答案;
(3)由(2)知當(dāng)![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,求得
上單調(diào)遞減,求得![]() ,
,
得到![]() ,令
,令![]() ,轉(zhuǎn)化為
,轉(zhuǎn)化為![]() 對
對![]() 恒成立,從而求出m的范圍.
恒成立,從而求出m的范圍.
(1)由題意得,函數(shù)![]() 定義域為
定義域為![]() ,
,
當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() ,則
,則![]() ,
,
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
所以當(dāng)![]() 時,
時,![]() 有極小值為
有極小值為![]() .
.
(2)當(dāng)![]() 時,求得函數(shù)的導(dǎo)數(shù)
時,求得函數(shù)的導(dǎo)數(shù)![]()
當(dāng)![]() 時,解得
時,解得![]() 和
和![]() .
.
①當(dāng)![]() 時,
時,![]() 恒成立,此時
恒成立,此時![]() 在
在![]() 上遞減;
上遞減;
②當(dāng)![]() ,即
,即![]() 時,
時,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上遞增,在
上遞增,在![]() 和
和![]() 上遞減;
上遞減;
③當(dāng)![]() ,即
,即![]() 時,
時,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() 在
在![]() 上遞增,在
上遞增,在![]() 和
和![]() 上遞減.
上遞減.
(3)由(2)知當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() ,
,
要使對任意![]() ,恒有
,恒有![]() 成立
成立
則有![]() ,
,
即![]() 對任意
對任意![]() 成立,即
成立,即![]() 對任意
對任意![]() 成立,
成立,
令![]() ,則
,則![]() 對
對![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調(diào)遞增,所以
上單調(diào)遞增,所以![]() ,
,
故m的取值范圍為![]() .
.


 輕松暑假總復(fù)習(xí)系列答案
輕松暑假總復(fù)習(xí)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】己知函數(shù)![]() 是函數(shù)值不恒為零的奇函數(shù),函數(shù)
是函數(shù)值不恒為零的奇函數(shù),函數(shù)![]() .
.
(1)求實數(shù)![]() 的值,并判斷函數(shù)
的值,并判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)解關(guān)于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“2019年”是一個重要的時間節(jié)點——中華人民共和國成立70周年,和全面建成小康社會的 關(guān)鍵之年.70年披荊斬棘,70年砥礪奮進(jìn),70年風(fēng)雨兼程,70年滄桑巨變,勤勞勇敢的中國 人用自己的雙手創(chuàng)造了一項項輝煌的成績,取得了舉世矚目的成就.趁此良機(jī),李明在天貓網(wǎng)店銷售“新中國成立70周年紀(jì)念冊”,每本紀(jì)念冊進(jìn)價4元,物流費、管理費共為![]() 元/本,預(yù)計當(dāng)每本紀(jì)念冊的售價為
元/本,預(yù)計當(dāng)每本紀(jì)念冊的售價為![]() 元(
元(![]() 時,月銷售量為
時,月銷售量為![]() 千本.
千本.
(I)求月利潤![]() (千元)與每本紀(jì)念冊的售價X的函數(shù)關(guān)系式,并注明定義域:
(千元)與每本紀(jì)念冊的售價X的函數(shù)關(guān)系式,并注明定義域:
(II)當(dāng)![]() 為何值時,月利潤
為何值時,月利潤![]() 最大?并求出最大月利潤.
最大?并求出最大月利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知A、B、C是△ABC的三個內(nèi)角,向量m=(-1, ![]() ),n=(cosA,sinA),且m·n=1.
),n=(cosA,sinA),且m·n=1.
(1)求角A;
(2)若![]() =-3,求tanC.
=-3,求tanC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() ,側(cè)面
,側(cè)面![]() 底面
底面![]() ,
,![]() .
.
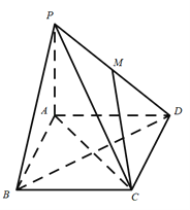
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若點![]() 為
為![]() 中點,求直線
中點,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 是定義在
是定義在![]() 上的偶函數(shù),且滿足
上的偶函數(shù),且滿足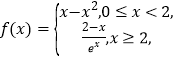 若函數(shù)
若函數(shù)![]() 有六個零點,則實數(shù)
有六個零點,則實數(shù)![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() :
:![]() 與直線
與直線![]() :
:![]() 的距離為
的距離為![]() ,橢圓
,橢圓![]() :
:![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)在(1)的條件下,拋物線![]() :
:![]() 的焦點
的焦點![]() 與點
與點![]() 關(guān)于
關(guān)于![]() 軸上某點對稱,且拋物線
軸上某點對稱,且拋物線![]() 與橢圓
與橢圓![]() 在第四象限交于點
在第四象限交于點![]() ,過點
,過點![]() 作拋物線
作拋物線![]() 的切線,求該切線方程并求該直線與兩坐標(biāo)軸圍成的三角形面積.
的切線,求該切線方程并求該直線與兩坐標(biāo)軸圍成的三角形面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com