
�o���E�A ��
��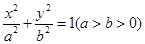 ���Q�A����ԭ�c(di��n)
���Q�A����ԭ�c(di��n)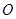 ���돽��
���돽��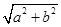 �ĈA�ǙE�A
�ĈA�ǙE�A �ġ���(zh��n)�A��.���E�A
�ġ���(zh��n)�A��.���E�A ��һ��(g��)���c(di��n)��
��һ��(g��)���c(di��n)��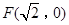 ������S�ϵ�һ��(g��)���c(di��n)��
������S�ϵ�һ��(g��)���c(di��n)��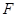 �ľ��x��
�ľ��x�� .
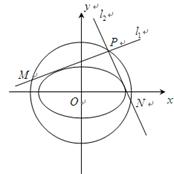
.
��1����E�A �ķ��̺��䡰��(zh��n)�A�����̣�
�ķ��̺��䡰��(zh��n)�A�����̣�
��2���c(di��n)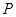 �ǙE�A
�ǙE�A �ġ���(zh��n)�A���ϵĄ�(d��ng)�c(di��n)���^�c(di��n)
�ġ���(zh��n)�A���ϵĄ�(d��ng)�c(di��n)���^�c(di��n)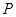 ���E�A���о�
���E�A���о�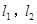 ������(zh��n)�A�����c(di��n)
������(zh��n)�A�����c(di��n)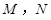 .
.
��������(d��ng)�c(di��n)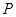 �顰��(zh��n)�A���c
�顰��(zh��n)�A���c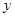 �S�����S�Ľ��c(di��n)�r(sh��)����ֱ��
�S�����S�Ľ��c(di��n)�r(sh��)����ֱ��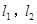 �ķ��̲��C��
�ķ��̲��C��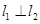 ��
��
���������C������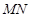 ���L�鶨ֵ.
���L�鶨ֵ.
��1��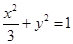 ,
,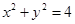 ,��2��������
,��2��������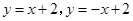 ��������ԔҊ����.
��������ԔҊ����.
����ԇ�}��������1����E�A���̣����ô���ϵ��(sh��)�����Ѓɂ�(g��)��(d��)�����̾Ϳɽ��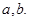 ��?y��n)���S�ϵ�һ��(g��)���c(di��n)��
��?y��n)���S�ϵ�һ��(g��)���c(di��n)��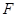 �ľ��x��
�ľ��x�� ������
������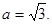 ��
��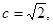 ����
����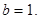 �ٸ���(j��)����(zh��n)�A�����x����������(zh��n)�A������.��2��������ֱ���c�E�A���І��}��ͨ�������Єeʽ�������о����̣������c(di��n)бʽ�O(sh��)ֱ�����̣��c�E�A����(li��n)����
�ٸ���(j��)����(zh��n)�A�����x����������(zh��n)�A������.��2��������ֱ���c�E�A���І��}��ͨ�������Єeʽ�������о����̣������c(di��n)бʽ�O(sh��)ֱ�����̣��c�E�A����(li��n)���� ���P(gu��n)��
���P(gu��n)��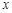 ��һԪ���η��̣����Єeʽ�����б��
��һԪ���η��̣����Єeʽ�����б��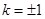 ,���C�Ã�ֱ����ֱ.���������}�ǣ�������һ�㻯�����Ȍ�(du��)б���Ƿ�����M(j��n)��ӑՓ��̽ӑ��б�ʲ����ڕr(sh��)�Ѓ�ֱ����ֱ���������}�D(zhu��n)�����о�ֱ���Ƿ�ֱ���}�����w�����о�
,���C�Ã�ֱ����ֱ.���������}�ǣ�������һ�㻯�����Ȍ�(du��)б���Ƿ�����M(j��n)��ӑՓ��̽ӑ��б�ʲ����ڕr(sh��)�Ѓ�ֱ����ֱ���������}�D(zhu��n)�����о�ֱ���Ƿ�ֱ���}�����w�����о�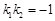 �Ƿ����.�о�˼·�ͷ���ͬ�������������c(di��n)
�Ƿ����.�о�˼·�ͷ���ͬ�������������c(di��n)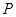 ����(bi��o)��׃�����������Єeʽ������P(gu��n)���c(di��n)
����(bi��o)��׃�����������Єeʽ������P(gu��n)���c(di��n)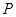 ����(bi��o)��һ��(g��)��ʽ��
����(bi��o)��һ��(g��)��ʽ��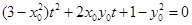 ����
����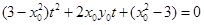 �����@��ʽ��(du��)�ɗl�о����m�ã�����
�����@��ʽ��(du��)�ɗl�о����m�ã����� ��б�ʞ鷽��
��б�ʞ鷽��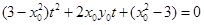 �ɸ������
�ɸ������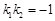 .��(d��ng)
.��(d��ng) ��ֱ�r(sh��)������
��ֱ�r(sh��)������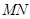 ���(zh��n)�A
���(zh��n)�A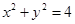 ��ֱ�����鶨ֵ4.
��ֱ�����鶨ֵ4.
ԇ�}�������⣺��1��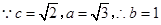 ��
��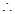 �E�A���̞�
�E�A���̞�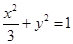 �� 2��
�� 2��
��(zh��n)�A���̞�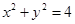 . 3��
. 3��
��2����������?y��n)�?zh��n)�A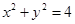 �c
�c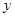 �S�����S�Ľ��c(di��n)��
�S�����S�Ľ��c(di��n)��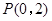 ��
��
�O(sh��)�^�c(di��n)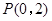 ���c�E�A���е�ֱ����
���c�E�A���е�ֱ����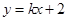 ��
��
������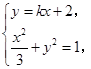 ��
��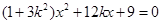 .
.
��?y��n)�ֱ��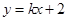 �c�E�A���У�
�c�E�A����
���� �����
�����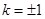 �� 6��
�� 6��
���� ���̞�
���̞�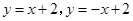 . 7��
. 7��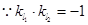 ��
��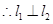 . 8��
. 8��
�������ٮ�(d��ng)ֱ�� ����һ�lб�ʲ����ڕr(sh��)�������O(sh��)ֱ��
����һ�lб�ʲ����ڕr(sh��)�������O(sh��)ֱ��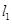 б�ʲ����ڣ�
б�ʲ����ڣ�
�t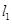 ��
��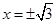 ��
��
��(d��ng)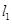 ��
��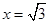 �r(sh��)��
�r(sh��)��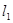 �c��(zh��n)�A�����c(di��n)
�c��(zh��n)�A�����c(di��n)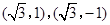 ��
��
�˕r(sh��)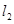 ��
��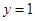 ����
����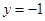 �����@Ȼֱ��
�����@Ȼֱ�� ��ֱ��
��ֱ��
ͬ�����C��(d��ng)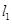 ��
��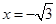 �r(sh��)��ֱ��
�r(sh��)��ֱ�� ��ֱ. 10��
��ֱ. 10��
�ڮ�(d��ng)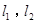 б�ʴ��ڕr(sh��)���O(sh��)�c(di��n)
б�ʴ��ڕr(sh��)���O(sh��)�c(di��n)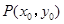 ������
������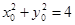 .
.
�O(sh��)��(j��ng)�^�c(di��n)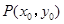 �c�E�A���е�ֱ����
�c�E�A���е�ֱ����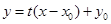 ��
��
������


| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�c(di��n)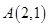 �ڒ��タ
�ڒ��タ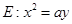 �ϣ�ֱ��
�ϣ�ֱ��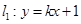 ��
�� ����
����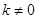 ���c���タ
���c���タ ���ཻ��
���ཻ��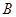 ��
�� ���c(di��n)��ֱ��
���c(di��n)��ֱ�� ��
�� �քe��ֱ��
�քe��ֱ��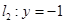 ���c(di��n)
���c(di��n) ��
��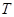 .
.
��1����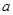 ��ֵ��
��ֵ��
��2����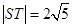 ����ֱ��
����ֱ�� �ķ��̣�
�ķ��̣�
��3��ԇ�Д��Ծ���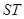 ��ֱ���ĈA�Ƿ���^�ɂ�(g��)���c(di��n)�����ǣ����@�ɂ�(g��)���c(di��n)������(bi��o)�������ǣ��f������.
��ֱ���ĈA�Ƿ���^�ɂ�(g��)���c(di��n)�����ǣ����@�ɂ�(g��)���c(di��n)������(bi��o)�������ǣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D���E�AC��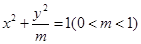 ������c(di��n)��A��M�ǙE�AC�Ϯ����c(di��n)A������һ�c(di��n)���c(di��n)P�c�c(di��n)A�P(gu��n)���c(di��n)M��(du��)�Q.
������c(di��n)��A��M�ǙE�AC�Ϯ����c(di��n)A������һ�c(di��n)���c(di��n)P�c�c(di��n)A�P(gu��n)���c(di��n)M��(du��)�Q.
��1�����c(di��n)P������(bi��o)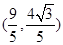 ����m��ֵ��
����m��ֵ��
��2�����E�AC�ϴ����c(di��n)M��ʹ��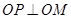 ����m��ȡֵ����.
����m��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A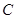 ��
�� ���x���ʞ�
���x���ʞ�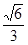 ���ҽ��c(di��n)��(
���ҽ��c(di��n)��( ��0)��
��0)��
(1)��E�A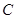 �ķ��̣�
�ķ��̣�
(2)���^ԭ�c(di��n)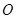 ���ɗl���ഹֱ���侀���c�E�A����
���ɗl���ഹֱ���侀���c�E�A����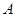 ��
��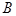 ���c(di��n)�����C���c(di��n)
���c(di��n)�����C���c(di��n)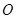 ��ֱ��
��ֱ��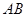 �ľ��x�鶨ֵ.
�ľ��x�鶨ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�A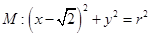
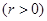 ,���E�A
,���E�A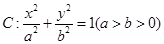 ������c(di��n)��A
������c(di��n)��A �ĈA�ģ��x���ʞ�
�ĈA�ģ��x���ʞ�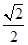 ��
��
��1����E�AC�ķ��̣�
��2��������ֱ��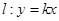 ��ʹ��ֱ��
��ʹ��ֱ�� �c�E�A
�c�E�A �քe����
�քe����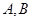 ���c(di��n)���c�A
���c(di��n)���c�A �քe����
�քe����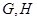 ���c(di��n)���c(di��n)
���c(di��n)���c(di��n)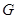 �ھ���
�ھ���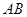 �ϣ���
�ϣ���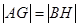 ����A
����A �İ돽
�İ돽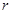 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�AC��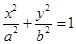 (
(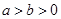 )�Ķ��S�L��2���x���ʞ�
)�Ķ��S�L��2���x���ʞ�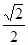
��1����E�AC�ķ���
��2�����^�c(di��n)M��2,0������б�ʞ�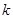 ��ֱ���c�E�AC�ཻ�ڃ��c(di��n)G��H���O(sh��)P��E�AC��һ�c(di��n)���ҝM��
��ֱ���c�E�AC�ཻ�ڃ��c(di��n)G��H���O(sh��)P��E�AC��һ�c(di��n)���ҝM��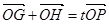 ��
��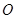 ������(bi��o)ԭ�c(di��n)������(d��ng)
������(bi��o)ԭ�c(di��n)������(d��ng)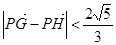 �r(sh��)����(sh��)��(sh��)
�r(sh��)����(sh��)��(sh��)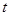 ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�E�A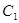 ���p����
���p����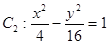 �Č�(sh��)�S����S��̓�S���L�S�����c���タ
�Č�(sh��)�S����S��̓�S���L�S�����c���タ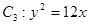 ����
���� ���c(di��n).
���c(di��n).
��1����E�A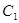 �ķ��̼�����
�ķ��̼�����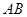 ���L��
���L��
��2����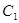 �c
�c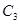 �D��Ĺ����^(q��)���(n��i)���Ƿ����һ�c(di��n)
�D��Ĺ����^(q��)���(n��i)���Ƿ����һ�c(di��n)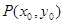 ��ʹ��
��ʹ��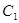 ����
����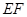 �c
�c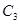 ����
����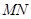 ���ֱƽ�����c(di��n)
���ֱƽ�����c(di��n)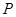 �������ڣ����c(di��n)
�������ڣ����c(di��n) ����(bi��o)���������ڣ��f������.
����(bi��o)���������ڣ��f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D����ƽ��ֱ������(bi��o)ϵxOy�У�M��N�քe�ǙE�A ��1����c(di��n)���^����(bi��o)ԭ�c(di��n)��ֱ�����E�A��P��A���c(di��n)������P�ڵ�һ���ޣ��^P��x�S�Ĵ����������C���B�Y(ji��)AC�������L���E�A���c(di��n)B���O(sh��)ֱ��PA��б�ʞ�k.
��1����c(di��n)���^����(bi��o)ԭ�c(di��n)��ֱ�����E�A��P��A���c(di��n)������P�ڵ�һ���ޣ��^P��x�S�Ĵ����������C���B�Y(ji��)AC�������L���E�A���c(di��n)B���O(sh��)ֱ��PA��б�ʞ�k.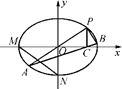
(1)��ֱ��PAƽ�־���MN����k��ֵ��
(2)��(d��ng)k��2�r(sh��)�����c(di��n)P��ֱ��AB�ľ��xd��
(3)��(du��)����k>0�����C��PA��PB..
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�AC�� ��1(a>b>0)���c(di��n)A��B�քe�ǙE�AC������c(di��n)������c(di��n)��ֱ��AB�c�AG��x2��y2��
��1(a>b>0)���c(di��n)A��B�քe�ǙE�AC������c(di��n)������c(di��n)��ֱ��AB�c�AG��x2��y2��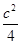 (c�ǙE�A�İ뽹��)���x��P��ֱ��AB��һ��(d��ng)�c(di��n)���^�c(di��n)P���AG�ă��о������c(di��n)�քe��M��N.
(c�ǙE�A�İ뽹��)���x��P��ֱ��AB��һ��(d��ng)�c(di��n)���^�c(di��n)P���AG�ă��о������c(di��n)�քe��M��N.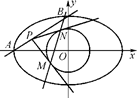
(1)���E�AC��(j��ng)�^���c(di��n)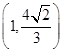 ��
��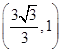 ����E�AC�ķ��̣�
����E�AC�ķ��̣�
(2)��(d��ng)c�鶨ֵ�r(sh��)�����C��ֱ��MN��(j��ng)�^һ���c(di��n)E������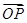 ��
��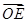 ��ֵ(O������(bi��o)ԭ�c(di��n))��
��ֵ(O������(bi��o)ԭ�c(di��n))��
(3)�������c(di��n)Pʹ�á�PMN���������Σ�ԇ��E�A�x���ʵ�ȡֵ������.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com