
【題目】已知函數f(x)=x3﹣ax,g(x)= ![]() x2﹣lnx﹣
x2﹣lnx﹣ ![]() .
.
(1)若f(x)和g(x)在同一點處有相同的極值,求實數a的值;
(2)對于一切x∈(0,+∞),有不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,求實數a的取值范圍;
(3)設G(x)= ![]() x2﹣
x2﹣ ![]() ﹣g(x),求證:G(x)>
﹣g(x),求證:G(x)> ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:∵g′(x)=x﹣ ![]() =
= ![]() ,∴當x∈(0,1)時,g'(x)<0,則g(x)單調遞減;當x∈(1,+∞)時,g'(x)>0,則g(x)單調遞增.∴g(x)極小值=g(1)=﹣2
,∴當x∈(0,1)時,g'(x)<0,則g(x)單調遞減;當x∈(1,+∞)時,g'(x)>0,則g(x)單調遞增.∴g(x)極小值=g(1)=﹣2
又∵f(x)和g(x)在同一點處有相同的極值,
∴f(1)=1﹣a=﹣2,即a=3
(2)解:若使對于一切x∈(0,+∞),不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,則只需使得不等式 ![]() 恒成立,即只需
恒成立,即只需 ![]()
設 ![]() ,則
,則 ![]() ,
,
∴當x∈(0,1)時,t'(x)<0,則t(x)單調遞減;當x∈(1,+∞)時,t'(x)>0,則t(x)單調遞增.
∴t(x)最小值=t(1)=4,
∴a≤4,即a的取值范圍為(﹣∞,4]
(3)解:若證 ![]() ,則只需證明
,則只需證明 ![]() ,即證
,即證 ![]()
設m(x)=xlnx,則m'(x)=lnx+1,由于m(x)在 ![]() 單調遞減,在
單調遞減,在 ![]() 單調遞增,所以
單調遞增,所以 ![]() ;設
;設 ![]() ,則
,則 ![]() ,由于n(x)在(0,1)單調遞增,在(1,+∞)單調遞減,所以
,由于n(x)在(0,1)單調遞增,在(1,+∞)單調遞減,所以 ![]() .
.
所以m(x)≥n(x)又由于m(x)與n(x)不在同一個變量時取得最值,即m(x)>n(x)
綜上所述, ![]()
【解析】(1)求出函數的導數,判斷導函數的符號,求出函數的極小值,然后列出方程求解a 即可.(2)使對于一切x∈(0,+∞),不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,轉化為 ![]() 恒成立,只需
恒成立,只需 ![]() ,構造函數,利用函數的導數求解函數的最小值,推出a的范圍即可.(3)若證
,構造函數,利用函數的導數求解函數的最小值,推出a的范圍即可.(3)若證 ![]() ,則只需證明
,則只需證明 ![]() ,即證
,即證 ![]() ,構造函數設m(x)=xlnx,利用函數的單調性求解函數的極值,推出結果即可.
,構造函數設m(x)=xlnx,利用函數的單調性求解函數的極值,推出結果即可.
【考點精析】利用函數的極值與導數對題目進行判斷即可得到答案,需要熟知求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(ωx+φ)(ω>0,﹣
sin(ωx+φ)(ω>0,﹣ ![]() <φ<
<φ< ![]() ),A(
),A( ![]() ,0)為f(x)圖象的對稱中心,B,C是該圖象上相鄰的最高點和最低點,若BC=4,則f(x)的單調遞增區(qū)間是( )
,0)為f(x)圖象的對稱中心,B,C是該圖象上相鄰的最高點和最低點,若BC=4,則f(x)的單調遞增區(qū)間是( )
A.(2k﹣ ![]() ,2k+
,2k+ ![]() ),k∈Z
),k∈Z
B.(2kπ﹣ ![]() π,2kπ+
π,2kπ+ ![]() π),k∈Z
π),k∈Z
C.(4k﹣ ![]() ,4k+
,4k+ ![]() ),k∈Z
),k∈Z
D.(4kπ﹣ ![]() π,4kπ+
π,4kπ+ ![]() π),k∈Z
π),k∈Z
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=eax(a≠0).
(1)當 ![]() 時,令
時,令 ![]() (x>0),求函數g(x)在[m,m+1](m>0)上的最小值;
(x>0),求函數g(x)在[m,m+1](m>0)上的最小值;
(2)若對于一切x∈R,f(x)﹣x﹣1≥0恒成立,求a的取值集合;
(3)求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象出現增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫(yī)院隨機的對入院50人進行了問卷調查得到了如下的列聯表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | 5 | ||
女 | 10 | ||
合計 | 50 |
已知在全部50人中隨機抽取1人,抽到患心肺疾病的人的概率為 ![]() .
.
(Ⅰ)請將上面的列聯表補充完整;
(Ⅱ)是否有99.5%的把握認為患心肺疾病與性別有關?說明你的理由;
(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.現在從患心肺疾病的10位女性中,選出3名進行其他方面的排查,記選出患胃病的女性人數為ξ,求ξ的分布列,數學期望以及方差;大氣污染會引起各種疾病,試淺談日常生活中如何減少大氣污染.
下面的臨界值表供參考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式K2= ![]() 其中n=a+b+c+d)
其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數y=f(x)滿足:①對于任意的x∈R,都有f(x+2)=f(x﹣2);②函數y=f(x+2)是偶函數;③當x∈(0,2]時,f(x)=ex﹣ ![]() ,a=f(﹣5),b=f(
,a=f(﹣5),b=f( ![]() ).c=f(
).c=f( ![]() ),則a,b,c的大小關系是( )
),則a,b,c的大小關系是( )
A.a<b<c
B.c<a<b
C.c<a<b
D.b<a<c
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a和b是任意非零實數.
(1)求 ![]() 的最小值.
的最小值.
(2)若不等式|2a+b|+|2a﹣b|≥|a|(|2+x|+|2﹣x|)恒成立,求實數x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,側棱AA1⊥底面A1B1C1 , AA1=AC=BC=1,∠ACB=90°,D是A1B1的中點,F是BB1上的點,AB1 , DF交于點E,且AB1⊥DF,則下列結論中不正確的是( ) 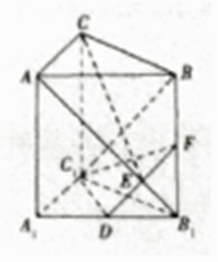
A.CE與BC1異面且垂直
B.AB1⊥C1F
C.△C1DF是直角三角形
D.DF的長為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點(a,b)是區(qū)域 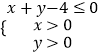 內的任意一點,則使函數f(x)=ax2﹣2bx+3在區(qū)間[
內的任意一點,則使函數f(x)=ax2﹣2bx+3在區(qū)間[ ![]() ,+∞)上是增函數的概率為( )
,+∞)上是增函數的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com