
【題目】在某校舉行的一次數(shù)學(xué)競賽中,全體參賽學(xué)生的競賽成績X近似服從正態(tài)分布N(70,100).已知成績在90分以上(含90分)的學(xué)生有16名.
(1)試問此次參賽的學(xué)生總數(shù)約為多少人?
(2)若該校計劃獎勵競賽成績在80分以上(含80分)的學(xué)生,試問此次競賽獲獎勵的學(xué)生約為多少人?
附:P(|X-μ|<σ)=0.683,P(|X-μ|<2σ)=0.954,P(|X-μ|<3σ)=0.997
【答案】(1)696 (2)110
【解析】試題分析:(1)由題意首先確定正態(tài)分布中μ,σ的值,然后結(jié)合正態(tài)分布的性質(zhì)求解參賽人數(shù)即可;
(2)利用(1)的結(jié)論結(jié)合正態(tài)分布圖象的對稱性即可確定需要獎勵的學(xué)生人數(shù).
試題解析:
設(shè)參賽學(xué)生的成績?yōu)?/span>X,因為X~N(70,100),所以μ=70,σ=10,則
![]()
![]() ,
,
16÷0.023≈696(人).
因此,此次參賽學(xué)生的總數(shù)約為696人.
(2)由P(X≥80)=P(X≤60)![]()
得696×0.1585≈110.
因此,此次競賽獲獎勵的學(xué)生約為110人.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列 ![]() 的各項均為正整數(shù),對于任意n∈N* , 都有
的各項均為正整數(shù),對于任意n∈N* , 都有 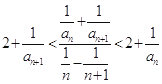 成立,且
成立,且 ![]() .
.
(1)求 ![]() ,
, ![]() 的值;
的值;
(2)猜想數(shù)列 ![]() 的通項公式,并給出證明.
的通項公式,并給出證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=lg(1﹣x)的定義域為M,函數(shù) ![]() 的定義域為N,則M∩N=( )
的定義域為N,則M∩N=( )
A.{x|x<1且x≠0}
B.{x|x≤1且x≠0}
C.{x|x>1}
D.{x|x≤1}
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的不等式![]() (其中
(其中![]() )。
)。
(1)當(dāng)a=4時,求不等式的解集;
(2)若不等式有解,求實數(shù)a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)r是方程f(x)=0的根,選取x0作為r的初始近似值,過點(x0,f(x0))做曲線y=f(x)的切線l,l的方程為y=f(x0)+![]() (x-x0),求出l與x軸交點的橫坐標(biāo)x1=x0-
(x-x0),求出l與x軸交點的橫坐標(biāo)x1=x0-![]() ,稱x1為r的一次近似值。過點(x1,f(x1))做曲線y=f(x)的切線,并求該切線與x軸交點的橫坐標(biāo)x2=x1-
,稱x1為r的一次近似值。過點(x1,f(x1))做曲線y=f(x)的切線,并求該切線與x軸交點的橫坐標(biāo)x2=x1-![]() ,稱x2為r的二次近似值。重復(fù)以上過程,得r的近似值序列,其中,
,稱x2為r的二次近似值。重復(fù)以上過程,得r的近似值序列,其中,![]() =
=![]() -
-![]() ,稱為r的n+1次近似值,上式稱為牛頓迭代公式。已知
,稱為r的n+1次近似值,上式稱為牛頓迭代公式。已知![]() 是方程
是方程![]() -6=0的一個根,若取x0=2作為r的初始近似值,則在保留四位小數(shù)的前提下,
-6=0的一個根,若取x0=2作為r的初始近似值,則在保留四位小數(shù)的前提下,![]() ≈
≈
A. 2.4494 B. 2.4495 C. 2.4496 D. 2.4497
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)設(shè)函數(shù)![]() .
.
(Ⅰ)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(Ⅱ)當(dāng)函數(shù)![]() 有最大值且最大值大于
有最大值且最大值大于![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為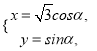 (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,以
為參數(shù)),以坐標(biāo)原點為極點,以![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出![]() 的普通方程和
的普通方程和![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】把一副三角板ABC與ABD擺成如圖所示的直二面角D﹣AB﹣C,(其中BD=2AD,BC=AC)則異面直線DC,AB所成角的正切值為( ) 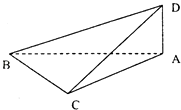
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() ,(a為常數(shù)且a>0).
,(a為常數(shù)且a>0).
(1)若函數(shù)的定義域為 ![]() ,值域為
,值域為 ![]() ,求a的值;
,求a的值;
(2)在(1)的條件下,定義區(qū)間(m,n),[m,n],(m,n],[m,n)的長度為n﹣m,其中n>m,若不等式f(x)+b>0,x∈[0,π]的解集構(gòu)成的各區(qū)間的長度和超過 ![]() ,求b的取值范圍.
,求b的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com