【題目】解關于x的方程：
（1）lgx+lg（x﹣3）=1；
（2）
．
【答案】
（1）解：∵lgx+lg（x﹣3）=lg[x（x﹣3）]=lg（x2﹣3x）=1=lg10
∴x2﹣3x=10，∴x=﹣2或5
∵x＞0，∴x=5
（2）解： 
∴ 
，∴x=3
【解析】（1）將不等式轉化為對數的真數的運算，轉化為整式不等式解之；（2）利用指數的冪的運算解答．
【考點精析】根據題目的已知條件，利用函數的零點與方程根的關系的相關知識可以得到問題的答案，需要掌握二次函數的零點：（1）△＞0，方程 有兩不等實根，二次函數的圖象與 軸有兩個交點，二次函數有兩個零點;（2）△＝0，方程 有兩相等實根（二重根），二次函數的圖象與 軸有一個交點，二次函數有一個二重零點或二階零點;（3）△＜0，方程 無實根，二次函數的圖象與 軸無交點，二次函數無零點．
科目：高中數學 來源： 題型：
【題目】已知曲線C1，C2的極坐標方程分別為ρ＝2cosθ， 
，射線θ＝φ， 
， 
與曲線C1交于（不包括極點O）三點A，B，C．
（Ⅰ）求證： 
；
（Ⅱ）當
時，求點B到曲線C2上的點的距離的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數 
，且f（1）=2，f（2）=3． （I）若f（x）是偶函數，求出f（x）的解析式；
（II）若f（x）是奇函數，求出f（x）的解析式；
（III）在（II）的條件下，證明f（x）在區間 
上單調遞減．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,在多面體
中，底面
是邊長為2的菱形， 
，四邊形
是矩形，平面
平面
.
（1）在圖中畫出過點
的平面
，使得
平面
（必須說明畫法，不需證明）；
（2）若二面角
是
，求
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知正四棱柱的底面邊長為
，高為
，現從該正四棱柱的
個頂點中任取
個點.設隨機變量
的值為以取出的個點為頂點的三角形的面積.
（1）求概率
；
（2）求的分布列，并求其數學期望
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一次函數f（x）是R上的增函數，已知f[f（x）]=16x+5，g（x）=f（x）（x+m）．
（1）求f（x）；
（2）若g（x）在（1，+∞）單調遞增，求實數m的取值范圍；
（3）當x∈[﹣1，3]時，g（x）有最大值13，求實數m的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】每年的4月23日是“世界讀書日”,某校研究性學習小組為了解本校學生的閱讀情況,隨機調查了本校200名學生在這一天的閱讀時間
(單位:分鐘),將樣本數據整理后繪制成如圖的樣本頻率分布直方圖.
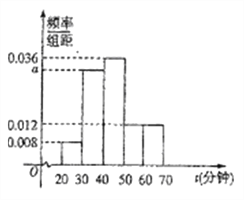
（1）求
的值；
（2）試估計該學校所有學生在這一天的平均閱讀時間；
（3）若用分層抽樣的方法從這200名學生中，抽出25人參加交流會，則閱讀時間為
， 
的兩組中各抽取多少人？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市文化部門為了了解本市市民對當地地方戲曲是否喜愛，從15-65歲的人群中隨機抽樣了
人，得到如下的統計表和頻率分布直方圖.
（1）寫出其中的
、
、
及
和
的值；
（2）若從第1，2，3組回答喜歡地方戲曲的人中用分層抽樣的方法抽取6人，求這三組每組分別抽取多少人？
（3）在（2）抽取的6人中隨機抽取2人，求這2人都是第3組的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
