
����С�}�M��12�֣�
��֪���� ��
�� ���O(sh��)����(sh��)
���O(sh��)����(sh��) ����
���� �ĈD���^�c(di��n)
�ĈD���^�c(di��n) ���c(di��n)
���c(di��n) .
.
������ ��ֵ��
��ֵ��
���� �ĈD������ƽ��
�ĈD������ƽ�� ��
�� ����(g��)��λ��õ�����(sh��)
����(g��)��λ��õ�����(sh��) �ĈD��.��
�ĈD��.�� �ĈD���ϸ�����c(di��n)���c(di��n)
�ĈD���ϸ�����c(di��n)���c(di��n) �ľ��x����Сֵ��1����
�ľ��x����Сֵ��1���� �Ć��{(di��o)���^(q��)�g.
���{(di��o)���^(q��)�g.
��I��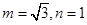 .
.
��II������(sh��) ���{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g�� .
.
����ԇ�}��������1�����}��֪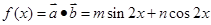 .
.
����(j��) �ĈD���^�c(di��n)
�ĈD���^�c(di��n) ��
�� ���õ�
���õ�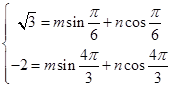 ��
��
���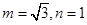 .
.
��2���ɣ�1��֪�� .
.
���}��֪��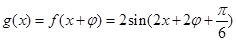 ��
��
���}��֪���c(di��n)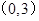 �ľ��x��1������c(di��n)��
�ľ��x��1������c(di��n)�� .
.
������� ��
��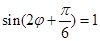 ��
��
�ɵ� ���õ�
���õ� ��
��
��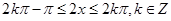 ����
����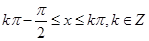 ��
��
�õ� �Ć��{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g�� .
.
ԇ�}��������1�����}��֪��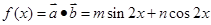 .
.
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/fb/1/ekb2s1.png" style="vertical-align:middle;" />�ĈD���^�c(di��n) ��
�� ��
��
����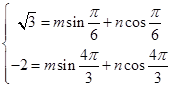 ��
��
�� ��
��
���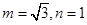 .
.
��2���ɣ�1��֪��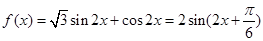 .
.
���}��֪��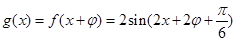 ��
��
�O(sh��) �ĈD���Ϸ����}�������c(di��n)��
�ĈD���Ϸ����}�������c(di��n)��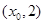 ��
��
���}��֪��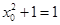 ������
������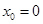 ��
��
�����c(di��n)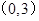 �ľ��x��1������c(di��n)��
�ľ��x��1������c(di��n)�� .
.
������� ��
��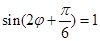 ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/f6/2/fdbmp1.png" style="vertical-align:middle;" />������ ��
��
��� ��
��
��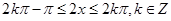 ����
����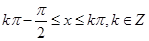 ��
��
���ԣ�����(sh��) �Ć��{(di��o)�f���^(q��)�g��
���{(di��o)�f���^(q��)�g�� .
.
���c(di��n)��ƽ�������Ĕ�(sh��)���e�����Ǻ���(sh��)�Ļ��������Ǻ���(sh��)�ĈD������|(zh��).



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪����(sh��)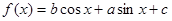 .
.
��1����(d��ng) �r(sh��)����
�r(sh��)���� ��ֵ��
��ֵ��
��2����(d��ng) ,
, �r(sh��)������(sh��)
�r(sh��)������(sh��) �ĈD���P(gu��n)��
�ĈD���P(gu��n)�� ���Q����(sh��)
���Q����(sh��)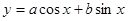 ���Q�S��
���Q�S��
��3���� �D������һ��(g��)����c(di��n)
�D������һ��(g��)����c(di��n) ������D����ÿ�c(di��n)�v����(bi��o)��׃���M����(bi��o)�s�̵�ԭ����
������D����ÿ�c(di��n)�v����(bi��o)��׃���M����(bi��o)�s�̵�ԭ���� ����Ȼ������ƽ��1��(g��)��λ�ɵ�
����Ȼ������ƽ��1��(g��)��λ�ɵ� �ĈD����֪
�ĈD����֪ ������������С�������Ξ�
������������С�������Ξ� ��
�� ����
���� ������
������ ����
���� �Ľ���ʽ.
�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
�O(sh��)����(sh��)f(x)��sin(2x����)(���У��գ�0)��y��f(x)�D���һ�l���Q�S��ֱ��x�� .
.
��1����գ�
��2����(sh��)y��f(x)���{(di��o)���^(q��)�g��
(3)��������(sh��)y��f(x)�څ^(q��)�g[0����]�ϵĈD��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪
��1����(sh��) ��ֵ��
��ֵ��
��2����(sh��) �����ֵ����Сֵ��
�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����(sh��) �IJ��ֈD����D��ʾ.
�IJ��ֈD����D��ʾ.
��1������ ����С�����ڼ��D��
����С�����ڼ��D�� ��
�� ��ֵ��
��ֵ��
��2���� �څ^(q��)�g
�څ^(q��)�g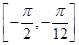 �ϵ����ֵ����Сֵ.
�ϵ����ֵ����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D,��һ�K�����΅^(q��)��ABCD,�F(xi��n)��Ҫ?ji��ng)���һ��(g��)ֱ��������AEF�^(q��)���M(j��n)�оG��,�M��:EF=1�ף��O(sh��)��AEF=��,�� ,߅��AE,AF,EF���M(f��i)�Þ�ÿ��1�fԪ,�^(q��)���(n��i)���M(f��i)�Þ�ÿƽ����4 �fԪ��
,߅��AE,AF,EF���M(f��i)�Þ�ÿ��1�fԪ,�^(q��)���(n��i)���M(f��i)�Þ�ÿƽ����4 �fԪ��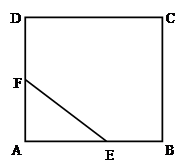
(1)���M(f��i)��y�P(gu��n)�ڦȵĺ���(sh��)��
(2)����С�Ŀ��M(f��i)�ú͌���(y��ng)�ȵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
ij��(sh��)�(y��n)��һ��Ĝضȣ���λ�� ���S�r(sh��)�g
���S�r(sh��)�g �����
����λ�� ����׃�����ƝM�㺯��(sh��)�P(gu��n)ϵ��
����׃�����ƝM�㺯��(sh��)�P(gu��n)ϵ�� .
.
��1����(sh��)�(y��n)���@һ������ز
��2����Ҫ��(sh��)�(y��n)�ҜضȲ�����11 ���t���ĶΕr(sh��)�g��(sh��)�(y��n)����Ҫ���أ�
���t���ĶΕr(sh��)�g��(sh��)�(y��n)����Ҫ���أ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
����AOB�����L��8 cm.
(1)���@��(g��)���ε���e��3 cm2����A�ĽǵĴ�С��
(2)���@��(g��)���ε���eȡ�����ֵ�r(sh��)�A�ĽǵĴ�С�����LAB.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��13�֣���2011•�ؑc���O(sh��)����(sh��)f��x��=sinxcosx��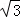 cos��x+�У�cosx����x��R��
cos��x+��cosx����x��R��
��I����f��x������С�����ڣ�
��II��������(sh��)y=f��x���ĈD�� =��
=�� ��
��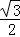 ��ƽ�ƺ�õ��ĺ���(sh��)y=g��x���ĈD����y=g��x���ڣ�0��
��ƽ�ƺ�õ��ĺ���(sh��)y=g��x���ĈD����y=g��x���ڣ�0�� ]�ϵ����ֵ��
]�ϵ����ֵ��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com