【題目】某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況，隨機在這兩條流水線上各抽取40件產品作為樣本，并稱出它們的重量（單位：克），重量值落在
內的產品為合格品，否則為不合格品，統計結果如表：
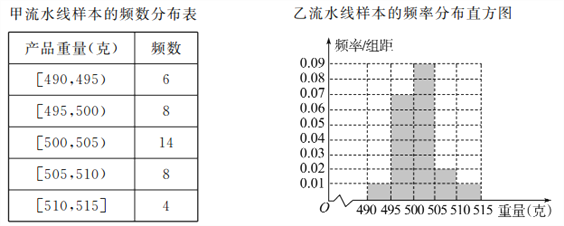
（Ⅰ）求甲流水線樣本合格的頻率；
（Ⅱ）從乙流水線上重量值落在
內的產品中任取2個產品，求這2件產品中恰好只有一件合格的概率．
【答案】（Ⅰ）0.75; （Ⅱ）
.
【解析】試題分析：（Ⅰ）首先計算落在
的頻數，頻數除以樣本容量就是頻率；（Ⅱ）根據頻率分布直方圖計算
和
的頻數，并且對產品編號，列舉任選兩件的基本事件，和恰有一件合格的基本事件的個數，計算其概率.
試題解析：（Ⅰ）由表知甲流水線樣本中合格品數為
，
故甲流水線樣本中合格品的頻率為
．
（Ⅱ）乙流水線上重量值落在
內的合格產品件數為
，
不合格產品件數為
．
設合格產品的編號為
， 
， 
， 
，不合格產品的編號為
， 
．
抽取2件產品的基本事件空間為
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
共15個．
用
表示“２件產品恰好只有一件合格”這一基本事件，則
， 
， 
， 
， 
， 
， 
， 
共8個，
故所求概率
．
開心練習課課練與單元檢測系列答案
開心試卷期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】設函數f（x）=log4（4x+1）+ax（a∈R）．
（1）若函數f（x）是定義在R上的偶函數，求a的值；
（2）若不等式f（x）+f（﹣x）≥mt+m對任意x∈R，t∈[﹣2，1]恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
為慶祝“2017年中國長春國際馬拉松賽”，某單位在慶祝晚會中進行嘉賓現場抽獎活動.抽獎盒中裝有大小相同的6個小球，分別印有“長春馬拉松”和“美麗長春”兩種標志，搖勻后，規定參加者每次從盒中同時抽取兩個小球(登記后放回并搖勻)，若抽到的兩個小球都印有“長春馬拉松”即可中獎，并停止抽獎，否則繼續，但每位嘉賓最多抽取3次.已知從盒中抽取兩個小球不都是“美麗長春”標志的概率為
.
(Ⅰ)求盒中印有“長春馬拉松”標志的小球個數；
(Ⅱ)用η表示某位嘉賓抽獎的次數，求η的分布列和期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正方體ABCD﹣A1B1C1D1的棱長為1，線段B1D1上有兩個動點E，F，且EF= 
，給出下列結論：
（1）AC⊥BE；
（2）EF∥平面ABCD；
（3）三棱錐A﹣BEF的體積為定值；
（4）異面直線AE，BF所成的角為定值．
其中錯誤的結論有（ ）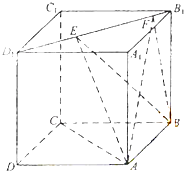
A.0個
B.1 個
C.2個
D.3個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】王府井百貨分店今年春節期間，消費達到一定標準的顧客可進行一次抽獎活動，隨著抽獎活動的有效開展，參與抽獎活動的人數越來越多，該分店經理對春節前7天參加抽獎活動的人數進行統計， 
表示第
天參加抽獎活動的人數，得到統計表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
經過進一步統計分析，發現
與
具有線性相關關系．
（1）請根據上表提供的數據，用最小二乘法求出
關于
的線性回歸方程
；
（2）判斷變量
與
之間是正相關還是負相關；
（3）若該活動只持續10天，估計共有多少名顧客參加抽獎．
參與公式： 
， 
， 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對應的邊分別為a，b，c，sinC+sin（A﹣B）=3sin2B．若 
，則 
=（ ）
A.
B.3
C. 或3
D.3或 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
