
【題目】設數列{an}的前n項和為Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且當n≥2時,4Sn+2+5Sn=8Sn+1+Sn-1.
,且當n≥2時,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)證明: ![]() 為等比數列.
為等比數列.
【答案】(1) ![]() ;(2)詳見解析.
;(2)詳見解析.
【解析】試題分析:(1)由題意令![]() ,把數列的和用項的形式列出,代入已知求出
,把數列的和用項的形式列出,代入已知求出![]() ;(2)由已知拆項,化簡為數列的遞推關系式形式,由等比數列的定義以及
;(2)由已知拆項,化簡為數列的遞推關系式形式,由等比數列的定義以及![]() 代入,即可證明.
代入,即可證明.
試題解析:
(1)解:當n=2時,4S4+5S2=8S3+S1,即4![]() +5
+5![]() =8
=8![]() +1,解得a4=
+1,解得a4=![]() .
.
(2)證明:由4Sn+2+5Sn=8Sn+1+Sn-1(n≥2),得4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2),即4an+2+an=4an+1(n≥2).
因為 4a3+a1=4×![]() +1=6=4a2,
+1=6=4a2,
所以 4an+2+an=4an+1,
所以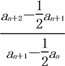 =
=![]() =
=![]() =
=
![]() =
=![]() ,
,
所以 數列![]() 是以a2-
是以a2-![]() a1=1為首項,
a1=1為首項,![]() 為公比的等比數列.
為公比的等比數列.
點睛: 等比數列的判斷方法有:(1)定義法:若![]() (
(![]() 為非零常數)或
為非零常數)或![]() (
(![]() 為非零常數且
為非零常數且![]() 且
且![]() ),則
),則![]() 是等比數列.(2)中項公式法:在數列
是等比數列.(2)中項公式法:在數列![]() 中,
中, ![]() 且
且![]() (
(![]() ),則數列
),則數列![]() 是等比數列.(3)通項公式法:若數列通項公式可寫成
是等比數列.(3)通項公式法:若數列通項公式可寫成![]() (
(![]() ,
, ![]() 均是不為0的常數,
均是不為0的常數, ![]() ),則
),則![]() 是等比數列.
是等比數列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,點![]() 是橢圓
是橢圓![]() 的一個頂點,
的一個頂點, ![]() 的長軸是圓
的長軸是圓![]() 的直徑.
的直徑. ![]() 是過點
是過點![]() 且互相垂直的兩條直線,其中
且互相垂直的兩條直線,其中![]() 交圓
交圓![]() 于兩點
于兩點![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 面積取最大值時直線
面積取最大值時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() ,數列
,數列![]() 滿足
滿足![]() 點
點![]() 在直線
在直線![]() 上.
上.
(1)求數列![]() ,
, ![]() 的通項
的通項![]() ,
, ![]() ;
;
(2)令![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)若![]() ,求對所有的正整數
,求對所有的正整數![]() 都有
都有![]() 成立的
成立的![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一袋中裝有6個黑球,4個白球.如果不放回地依次取出2個球.求:
(1)第1次取到黑球的概率;
(2)第1次和第2次都取到黑球的概率;
(3)在第1次取到黑球的條件下,第2次又取到黑球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,ABCD﹣A1B1C1D1是棱長為a的正方體,M、N分別是下底面的棱A1B1 , B1C1的中點,P是上底面的棱AD上的一點,AP= ![]() ,過P、M、N的平面交上底面于PQ,Q在CD上,則PQ= .
,過P、M、N的平面交上底面于PQ,Q在CD上,則PQ= . 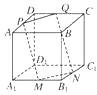
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn,已知a1=10,a2為整數,且Sn≤S4.
(1)求{an}的通項公式;
(2)設bn=![]() ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為非零常數.
為非零常數.
(1)若![]() ,
, ![]() ,求證:
,求證: ![]() 為等比數列,并求數列
為等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 是公差不等于零的等差數列.
是公差不等于零的等差數列.
①求實數![]() ,
, ![]() 的值;
的值;
②數列![]() 的前
的前![]() 項和
項和![]() 構成數列
構成數列![]() ,從
,從![]() 中取不同的四項按從小到大排列組成四項子數列.試問:是否存在首項為
中取不同的四項按從小到大排列組成四項子數列.試問:是否存在首項為![]() 的四項子數列,使得該子數列中的所有項之和恰好為2017?若存在,求出所有滿足條件的四項子數列;若不存在,請說明理由.
的四項子數列,使得該子數列中的所有項之和恰好為2017?若存在,求出所有滿足條件的四項子數列;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙“十一”結束之后,某網站針對購物情況進行了調查,參與調查的人主要集中在[20,50]歲之間,若規定:購物600(含600元)以下者,稱為“理智購物”,購物超過600元者被網友形象的稱為“剁手黨”,得到如下統計表:
分組編號 | 年齡分組 | 球迷 | 所占比例 |
1 | [20,25) | 1000 | 0.5 |
2 | [25,30) | 1800 | 0.6 |
3 | [30,35) | 1200 | 0.5 |
4 | [35,40) | a | 0.4 |
5 | [40,45) | 300 | 0.2 |
6 | [45,50] | 200 | 0.1 |
若參與調查的“理智購物”總人數為7720人.
(1)求a的值;
(2)從年齡在[20,35)的“剁手黨”中按照年齡區間分層抽樣的方法抽取20人; ①從這20人中隨機抽取2人,求這2人恰好屬于同一年齡區間的概率;
②從這20人中隨機抽取2人,用ζ表示年齡在[20,25)之間的人數,求ξ的分布列及期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為0的等差數列{an}的前n項和為Sn, S3=a4+6,且a1, a4, a13成等比數列.
(1)求數列{an}的通項公式;
(2)設![]() ,求數列{bn}的前n項和.
,求數列{bn}的前n項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com