
【題目】(本題共12分)已知函數(shù)![]()
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)是否存在常數(shù)![]() ,使
,使![]() 對任意的
對任意的![]() 和任意的
和任意的![]() 都成立,若存在,求出t的取值范圍;若不存在,請說明理由.
都成立,若存在,求出t的取值范圍;若不存在,請說明理由.
【答案】(1)詳見解析(2)![]()
【解析】試題分析:
(1)首先對函數(shù)![]() 求導(dǎo),結(jié)合定義域在
求導(dǎo),結(jié)合定義域在![]() ,對參數(shù)
,對參數(shù)![]() 小于等于0,和大于0兩種情況進(jìn)行討論。
小于等于0,和大于0兩種情況進(jìn)行討論。
(2)恒成立問題,首先求出![]() 在
在![]() 上的最小值
上的最小值![]() ,再求出
,再求出![]() 的最小值,從而求出t的范圍
的最小值,從而求出t的范圍
試題解析:
(1)![]()
![]() ,
,
①當(dāng)![]() 時,
時, ![]() ,
, ![]()
![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;
上單調(diào)遞減;
②當(dāng)![]() 時,令
時,令![]() ,得
,得![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞增;
單調(diào)遞增;
綜上所得,當(dāng)![]() 時,
時, ![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞減;當(dāng)
上單調(diào)遞減;當(dāng)![]() 時,
時, ![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞減,
單調(diào)遞減, ![]() 在區(qū)間
在區(qū)間![]() 單調(diào)遞增
單調(diào)遞增
(2)![]()
![]()
![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞減;
單調(diào)遞減;
![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞增;
單調(diào)遞增;
![]()
又因為![]() 在
在![]() 單調(diào)遞減,且
單調(diào)遞減,且![]() ,
, ![]() ,
,
![]() 存在
存在![]() ,
, ![]() ,所以當(dāng)
,所以當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞增,當(dāng)
單調(diào)遞增,當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞減,所以
單調(diào)遞減,所以![]()
故![]()


 孟建平小學(xué)滾動測試系列答案
孟建平小學(xué)滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() 中心在原點,焦點在
中心在原點,焦點在![]() 軸上,
軸上, ![]() 、
、![]() 分別為上、下焦點,橢圓的離心率為
分別為上、下焦點,橢圓的離心率為![]() ,
, ![]() 為橢圓上一點且
為橢圓上一點且![]() .
.
(1)若![]() 的面積為
的面積為![]() ,求橢圓
,求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若![]() 的延長線與橢圓
的延長線與橢圓![]() 另一交點為
另一交點為![]() ,以
,以![]() 為直徑的圓過點
為直徑的圓過點 ,
, ![]() 為橢圓上動點,求
為橢圓上動點,求![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等比數(shù)列{an}中,a1=2,a4=16
(1)求數(shù)列{an}的通項公式;
(2)令 ![]() ,n∈N* , 求數(shù)列{bn}的前n項和Sn .
,n∈N* , 求數(shù)列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】經(jīng)銷商經(jīng)銷某種農(nóng)產(chǎn)品,在一個銷售季度內(nèi),每售出![]() 該產(chǎn)品獲利潤500元,未售出的產(chǎn)品,每
該產(chǎn)品獲利潤500元,未售出的產(chǎn)品,每![]() 虧損300元.根據(jù)歷史資料,得到銷售季度內(nèi)市場需求量的頻率分布直方圖,如圖所示.經(jīng)銷商為下一個銷售季度購進(jìn)了
虧損300元.根據(jù)歷史資料,得到銷售季度內(nèi)市場需求量的頻率分布直方圖,如圖所示.經(jīng)銷商為下一個銷售季度購進(jìn)了![]() 該農(nóng)產(chǎn)品.以
該農(nóng)產(chǎn)品.以![]() (單位:
(單位: ![]() )表示下一個銷售季度內(nèi)的市場需求量,
)表示下一個銷售季度內(nèi)的市場需求量, ![]() (單位:元)表示下一個銷售季度內(nèi)經(jīng)銷該農(nóng)產(chǎn)品的利潤.
(單位:元)表示下一個銷售季度內(nèi)經(jīng)銷該農(nóng)產(chǎn)品的利潤.
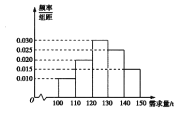
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)根據(jù)直方圖估計利潤![]() 不少于57000元的概率;
不少于57000元的概率;
(3)在直方圖的需求量分組中,以各組的區(qū)間中點值代表該組的各個值,并以需求量落入該區(qū)間的頻率作為需求量取該區(qū)間中點值的概率(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率),求
的頻率),求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù) ![]() 在R上可導(dǎo),其導(dǎo)函數(shù)為
在R上可導(dǎo),其導(dǎo)函數(shù)為 ![]() 且函數(shù)
且函數(shù) ![]() 的圖像如圖所示,則下列結(jié)論一定成立的是( )
的圖像如圖所示,則下列結(jié)論一定成立的是( ) 
A.函數(shù) ![]() 的極大值是
的極大值是 ![]() ,極小值是
,極小值是 ![]()
B.函數(shù) ![]() 的極大值是
的極大值是 ![]() ,極小值是
,極小值是 ![]()
C.函數(shù) ![]() 的極大值是
的極大值是 ![]() ,極小值是
,極小值是 ![]()
D.函數(shù) ![]() 的極大值是
的極大值是 ![]() ,極小值是
,極小值是 ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正三棱柱![]() 的各條棱長均相等,
的各條棱長均相等, ![]() 為
為![]() 的中點,
的中點, ![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() .當(dāng)
.當(dāng)![]() 運動時,下列結(jié)論中不正確的是( )
運動時,下列結(jié)論中不正確的是( )
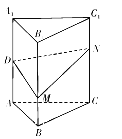
A. 平面![]() 平面
平面![]() B. 三棱錐
B. 三棱錐![]() 的體積為定值
的體積為定值
C. ![]() 可能為直角三角形 D. 平面
可能為直角三角形 D. 平面![]() 與平面
與平面![]() 所成的銳二面角范圍為
所成的銳二面角范圍為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某校舉行的數(shù)學(xué)競賽中,全體參賽學(xué)生的競賽成績近似地服從正態(tài)分布N(70,100).已知成績在90分以上的學(xué)生有12人.
(1)試問此次參賽學(xué)生的總數(shù)約為多少人?
(2)若成績在80分以上(含80分)為優(yōu),試問此次競賽成績?yōu)閮?yōu)的學(xué)生約為多少人?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線L經(jīng)過點P(﹣4,﹣3),且被圓(x+1)2+(y+2)2=25截得的弦長為8,則直線L的方程是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() ,其前
,其前![]() 項和為
項和為![]() .
.
(1)若對任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 組成公差為4的等差數(shù)列,且
組成公差為4的等差數(shù)列,且![]() ,求
,求![]() ;
;
(2)若數(shù)列 是公比為
是公比為![]() (
(![]() )的等比數(shù)列,
)的等比數(shù)列, ![]() 為常數(shù),
為常數(shù),
求證:數(shù)列![]() 為等比數(shù)列的充要條件為
為等比數(shù)列的充要條件為![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com