
【題目】已知M為△ABC的中線AD的中點,過點M的直線分別交兩邊AB、AC于點P、Q,設(shè) ![]() =x
=x ![]() ,
, ![]() ,記y=f(x).
,記y=f(x).
(1)求函數(shù)y=f(x)的表達式;
(2)設(shè)g(x)=x3+3a2x+2a,x∈[0,1].若對任意x1∈[ ![]() ,1],總存在x2∈[0,1],使得f(x1)=g(x2)成立,求實數(shù)a的取值范圍.
,1],總存在x2∈[0,1],使得f(x1)=g(x2)成立,求實數(shù)a的取值范圍.
【答案】
(1)解:∵過點M的直線分別交兩邊AB、AC于P、Q,
∴0<x≤1,0<y≤1
又∵ ![]() =x
=x ![]() ,
, ![]() =y
=y ![]() ,
,
∴ ![]() =
= ![]()
![]() =
= ![]() (
( ![]() +
+ ![]() )=
)= ![]()
![]() +
+ ![]()
![]()
又∵P、M、Q三點共線,
∴ ![]() +
+ ![]() =1,
=1,
∴y=f(x)= ![]()
由 ![]() 得
得 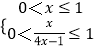 ,
,
∴ ![]() ≤x≤1,
≤x≤1,
∴y=f(x)= ![]() ,x∈[
,x∈[ ![]() ,1]
,1]
(2)解:∵f(x)= ![]() =
= ![]() +
+ ![]() 在[
在[ ![]() ,1]內(nèi)是減函數(shù),
,1]內(nèi)是減函數(shù),
∴[f(x)]min=f(1)= ![]() ,[f(x)]max=f(
,[f(x)]max=f( ![]() )=1,
)=1,
即函數(shù)f(x)的值域為[ ![]() ,1]
,1]
∵g'(x)=3x2+3a2≥0,
∴g(x)在[0,1]內(nèi)是增函數(shù),
∴[g(x)]min=g(0)=2a,[g(x)]max=g(1)=3a2+2a+1,
∴g(x)的值域為[2a,3a2+2a+1]
由題設(shè)得[ ![]() ,1][2a,3a2+2a+1],
,1][2a,3a2+2a+1],
則 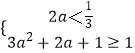
解得a的取值范圍是(﹣∞,﹣ ![]() ]∪[0,
]∪[0, ![]() ]
]
【解析】(1)表示出向量AM,根據(jù)P、M、Q三點共線,得到關(guān)于x,y的等式,解出y即f(x)的解析式;(2)分別根據(jù)f(x),g(x)的單調(diào)性,求出f(x),g(x)的值域,結(jié)合集合的包含關(guān)系得到關(guān)于a的不等式組,解出即可.
【考點精析】掌握平面向量的基本定理及其意義是解答本題的根本,需要知道如果![]() 、
、![]() 是同一平面內(nèi)的兩個不共線向量,那么對于這一平面內(nèi)的任意向量
是同一平面內(nèi)的兩個不共線向量,那么對于這一平面內(nèi)的任意向量![]() ,有且只有一對實數(shù)
,有且只有一對實數(shù)![]() 、
、![]() ,使
,使![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切.
,以原點為圓心,橢圓C的短半軸長為半徑的圓與直線x﹣y+2=0相切. 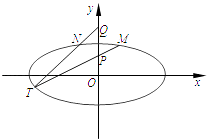
(1)求橢圓C的方程;
(2)已知點P(0,1),Q(0,2).設(shè)M,N是橢圓C上關(guān)于y軸對稱的不同兩點,直線PM與QN相交于點T,求證:點T在橢圓C上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=  ,若對任意的a∈(﹣3,+∞),關(guān)于x的方程f(x)=kx都有3個不同的根,則k等于( )
,若對任意的a∈(﹣3,+∞),關(guān)于x的方程f(x)=kx都有3個不同的根,則k等于( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=xex , g(x)=﹣(x+1)2+a,若x1 , x2∈R,使得f(x2)≤g(x1)成立,則實數(shù)a的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙等五名奧運志愿者被隨機地分到A,B,C,D四個不同的崗位服務(wù),每個崗位至少有一名志愿者.
(1)求甲、乙兩人同時參加A崗位服務(wù)的概率;
(2)求甲、乙兩人不在同一個崗位服務(wù)的概率;
(3)設(shè)隨機變量ξ為這五名志愿者中參加A崗位服務(wù)的人數(shù),求ξ的分布列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知F1 , F2分別為雙曲線 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右焦點,如果雙曲線上存在一點P,使得F2關(guān)于直線PF1的對稱點恰在y軸上,則該雙曲線的離心率e的取值范圍為( )
=1(a>0,b>0)的左右焦點,如果雙曲線上存在一點P,使得F2關(guān)于直線PF1的對稱點恰在y軸上,則該雙曲線的離心率e的取值范圍為( )
A.e> ![]()
B.1<e< ![]()
C.e> ![]()
D.1<e< ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我市某礦山企業(yè)生產(chǎn)某產(chǎn)品的年固定成本為![]() 萬元,每生產(chǎn)千件該產(chǎn)品需另投入
萬元,每生產(chǎn)千件該產(chǎn)品需另投入![]() 萬元,設(shè)該企業(yè)年內(nèi)共生產(chǎn)此種產(chǎn)品
萬元,設(shè)該企業(yè)年內(nèi)共生產(chǎn)此種產(chǎn)品![]() 千件,并且全部銷售完,每千件的銷售收入為
千件,并且全部銷售完,每千件的銷售收入為![]() 萬元,且
萬元,且
(Ⅰ)寫出年利潤![]() (萬元)關(guān)于產(chǎn)品年產(chǎn)量
(萬元)關(guān)于產(chǎn)品年產(chǎn)量![]() (千件)的函數(shù)關(guān)系式;
(千件)的函數(shù)關(guān)系式;
(Ⅱ)問:年產(chǎn)量![]() 為多少千件時,該企業(yè)生產(chǎn)此產(chǎn)品所獲年利潤最大?
為多少千件時,該企業(yè)生產(chǎn)此產(chǎn)品所獲年利潤最大?
注:年利潤=年銷售收入-年總成本.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a,b為正實數(shù),且 ![]() ,若a+b﹣c≥0對于滿足條件的a,b恒成立,則c的取值范圍為( )
,若a+b﹣c≥0對于滿足條件的a,b恒成立,則c的取值范圍為( )
A.![]()
B.(﹣∞,3]
C.(﹣∞,6]
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com