
科目: 來源: 題型:
【題目】中國武漢于2019年10月18日至2019年10月27日成功舉辦了第七屆世界軍人運動會.來自109個國家的9300余名運動員同臺競技.經過激烈的角逐,獎牌榜的前3名如下:
國家 | 金牌 | 銀牌 | 銅牌 | 獎牌總數 |
中國 | 133 | 64 | 42 | 239 |
俄羅斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某數學愛好者采用分層抽樣的方式,從中國和巴西獲得金牌選手中抽取了22名獲獎代表.從這22名中隨機抽取3人, 則這3人中中國選手恰好1人的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】在直角坐標系xOy下,曲線C1的參數方程為![]() (
(![]() 為參數),曲線C1在變換T:
為參數),曲線C1在變換T:![]() 的作用下變成曲線C2.
的作用下變成曲線C2.
(1)求曲線C2的普通方程;
(2)若m>1,求曲線C2與曲線C3:y=m|x|-m的公共點的個數.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() ,點
,點![]() ,過
,過![]() 的直線
的直線![]() 與圓
與圓![]() 交于點
交于點![]() ,過
,過![]() 做直線
做直線![]() 平行
平行![]() 交
交![]() 于點
于點![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過![]() 的直線與
的直線與![]() 交于
交于![]() 、
、![]() 兩點,若線段
兩點,若線段![]() 的中點為
的中點為![]() ,且
,且![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目: 來源: 題型:
【題目】根據養殖規模與以往的養殖經驗,某海鮮商家的海產品每只質量(克)在正常環境下服從正態分布![]() .
.
(1)隨機購買10只該商家的海產品,求至少買到一只質量小于![]() 克該海產品的概率.
克該海產品的概率.
(2)2020年該商家考慮增加先進養殖技術投入,該商家欲預測先進養殖技術投入為49千元時的年收益增量.現用以往的先進養殖技術投入![]() (千元)與年收益增量
(千元)與年收益增量![]() (千元)(
(千元)(![]() )的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線
)的數據繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線![]() 的附近,且
的附近,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,其中
,其中![]() ,
,![]() =
=![]()
![]() .根據所給的統計量,求
.根據所給的統計量,求![]() 關于
關于![]() 的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
的回歸方程,并預測先進養殖技術投入為49千元時的年收益增量.
附:若隨機變量![]() ,則
,則![]() ,
,![]() ;
;
對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為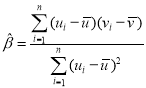 ,
,![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】中國武漢于2019年10月18日至2019年10月27日成功舉辦了第七屆世界軍人運動會.來自109個國家的9300余名運動員同臺競技.經過激烈的角逐,獎牌榜的前3名如下:
國家 | 金牌 | 銀牌 | 銅牌 | 獎牌總數 |
中國 | 133 | 64 | 42 | 239 |
俄羅斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某數學愛好者采用分層抽樣的方式,從中國和巴西獲得金牌選手中抽取了22名獲獎代表.從這22名中隨機抽取3人, 則這3人中中國選手恰好1人的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
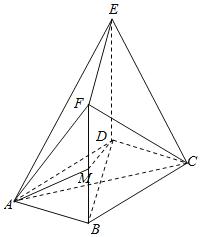
【題目】如圖,在多面體ABCDEF中,底面ABCD是邊長為2的菱形,∠BAD=60°,四邊形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M為線段BF上一點,且DM⊥平面ACE.
(1)求BM的長;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目: 來源: 題型:
【題目】數列{an}首項a1=1,前n項和Sn與an之間滿足an=![]()
(1)求證:數列{![]() }是等差數列
}是等差數列
(2)求數列{an}的通項公式
(3)設存在正數k,使(1+S1)(1+S2)…(1+Sn)≥k![]() 對于一切n∈N*都成立,求k的最大值.
對于一切n∈N*都成立,求k的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com