精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

【題目】《九章算術》是我國古代數學成就的杰出代表.其中《方田》章給出計算弧田面積的經驗公式為：.弧田（如圖1陰影部分）由圓弧和其所對弦圍成，弦”指圓弧所對弦長，“矢”等于半徑長與圓心到弦的距離之差.類比弧田面積公式得到球缺(如圖 2)近似體積公式：圓面積矢.球缺是指一個球被平面截下的一部分，廈門嘉庚體育館近似球缺結構（如圖3)，若該體育館占地面積約為18000，建筑容積約為340000，估計體育館建筑高度(單位：)所在區間為（ ）

參考數據: ，，，

，.

A. B. C. D.

【題目】在極坐標系中,直線的極坐標方程為．以極點為原點,極軸為軸的正半軸建立平面直角坐標系,曲線的參數方程為,（為參數）．

（1）請寫出直線的參數方程;

（2）求直線與曲線交點的直角坐標．

【題目】如圖,在三棱錐中,是等邊三角形,,點是 的中點,連接．

（1）證明:平面平面;

（2）若,且二面角為,求直線與平面所成角的正弦值．

【題目】已知函數.

（1）當時，求曲線在點處的切線方程；

（2）若，求證：.

【題目】2019年12月以來，湖北武漢市發現多起病毒性肺炎病例，并迅速在全國范圍內開始傳播，專家組認為，本次病毒性肺炎病例的病原體初步判定為新型冠狀病毒，該病毒存在人與人之間的傳染，可以通過與患者的密切接觸進行傳染.我們把與患者有過密切接觸的人群稱為密切接觸者，每位密切接觸者被感染后即被稱為患者.已知每位密切接觸者在接觸一個患者后被感染的概率為，某位患者在隔離之前，每天有位密切接觸者，其中被感染的人數為，假設每位密切接觸者不再接觸其他患者.

（1）求一天內被感染人數為的概率與、的關系式和的數學期望；

（2）該病毒在進入人體后有14天的潛伏期，在這14天的潛伏期內患者無任何癥狀，為病毒傳播的最佳時間，設每位患者在被感染后的第二天又有位密切接觸者，從某一名患者被感染，按第1天算起，第天新增患者的數學期望記為.

（i）求數列的通項公式，并證明數列為等比數列；

（ii）若戴口罩能降低每位密切接觸者患病概率，降低后的患病概率，當取最大值時，計算此時所對應的值和此時對應的值，根據計算結果說明戴口罩的必要性.（取）

（結果保留整數，參考數據：）

【題目】[2019·開封一模]已知數列中，，，利用下面程序框圖計算該數列的項時，若輸出的是2，則判斷框內的條件不可能是（ ）

A. B. C. D.

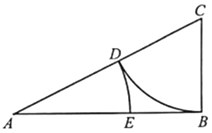
【題目】古希臘雅典學派算學家歐道克薩斯提出了“黃金分割”的理論，利用尺規作圖可畫出己知線段的黃金分割點，具體方法如下：（l）取線段AB＝2，過點B作AB的垂線，并用圓規在垂線上截取BC＝AB，連接AC；（2）以C為圓心，BC為半徑畫弧，交AC于點D；（3）以A為圓心，以AD為半徑畫弧，交AB于點E．則點E即為線段AB的黃金分割點．若在線段AB上隨機取一點F，則使得BE≤AF≤AE的概率約為（　　）（參考數據：2.236）

A. 0.236B. 0.382C. 0.472D. 0.618

（1）根據題意，填寫下面的2×2列聯表，并根據列聯表判斷是否有90%以上的把握認為“理科綜合”成績是否優秀與性別有關．

（2）用分層抽樣的方法從成績優秀的學生中隨機抽取12名學生，然后再從這12名學生中抽取3名參加某高校舉辦的自主招生考試，設抽到的3名學生中女生的人數為X，求X的分布列及數學期望．

附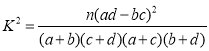：，其中．

【題目】如圖，在多面體中，四邊形是菱形，，四邊形是直角梯形，，，.

（Ⅰ）證明：平面.

（Ⅱ）若平面平面，為的中點，求平面與平面所成銳二面角的余弦值.

（1）當a＝4時，求解不等式f（x）≥8；

（2）已知關于x的不等式f（x）在R上恒成立，求參數a的取值范圍．