
���Kʡ�Ͼ���2009�ø�����һ���{(di��o)�п�ԇ
��(sh��)�W(xu��)ԇ�}2009.3
һ������}�������}��14С�}��ÿС�}5�֣���70�֣�
1��Ӌ(j��)�㣺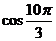 = ��
= ��
 2�����(f��)��(sh��)
2�����(f��)��(sh��)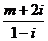
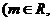
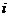 ��̓��(sh��)��λ���鼃̓��(sh��)���t
��̓��(sh��)��λ���鼃̓��(sh��)���t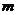 = ��
= ��
3��ij��5 ���ϰ�;�������ĕr(sh��)�g����λ����犣��քe��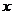 ��
�� ����֪�@�M��(sh��)��(j��)��ƽ����(sh��)��10���t�䷽��� ��
����֪�@�M��(sh��)��(j��)��ƽ����(sh��)��10���t�䷽��� ��
 4����֪�ȱȔ�(sh��)��
4����֪�ȱȔ�(sh��)�� �ĸ��(xi��ng)��������(sh��)����
�ĸ��(xi��ng)��������(sh��)����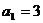 ��ǰ���(xi��ng)�ĺ͞�21 ��
��ǰ���(xi��ng)�ĺ͞�21 ��
 �t
�t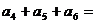 ��
��
 5���O(sh��)
5���O(sh��)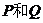 �ǃɂ�(g��)���ϣ����x����
�ǃɂ�(g��)���ϣ����x����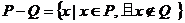 ����
����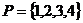 ��
��

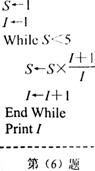
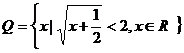 ���t
���t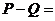 ��
��
 6������(j��)��D��ʾ�Ăδ��a����֪ݔ���ĽY(ji��)��
6������(j��)��D��ʾ�Ăδ��a����֪ݔ���ĽY(ji��)��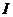 ��
��
��
��




 7����֪���ε����L��
7����֪���ε����L�� ���tԓ������e�����ֵ��
���tԓ������e�����ֵ��  ��
��
 8���^�E�A
8���^�E�A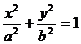
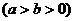 ������c(di��n)
������c(di��n) ��б�ʞ�
��б�ʞ� ��ֱ�����c�E�A����һ��(g��)���c(di��n)��
��ֱ�����c�E�A����һ��(g��)���c(di��n)�� ���c
���c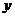 �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)��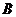 ����
����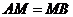 ���tԓ�E�A���x���ʞ�
��
���tԓ�E�A���x���ʞ�
��
 9��������
9��������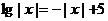 �څ^(q��)�g
�څ^(q��)�g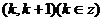 ���н⣬�t���НM��l����
���н⣬�t���НM��l���� ��ֵ�ĺ͞�
��
��ֵ�ĺ͞�
��




 10����D���������������5����������
10����D���������������5���������� ��
�� ������
������ λ�ڟ���
λ�ڟ��� �����Ϸ�����ͣ��������݆�����״�λ�ڟ���
�����Ϸ�����ͣ��������݆�����״�λ�ڟ��� �ı�ƫ��
�ı�ƫ��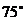 �����c
�����c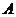 ���
���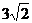 �����
�����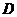 ̎���Ҵ�λ�ڟ���B�ı�ƫ��
̎���Ҵ�λ�ڟ���B�ı�ƫ��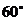 �����c
�����c ���5�����
���5����� ̎���t���Ҵ�֮�g�ľ��x�� ���
̎���t���Ҵ�֮�g�ľ��x�� ���

 11����D������������
11����D������������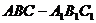 ��D����
��D���� �����c(di��n)��������
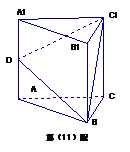
�����c(di��n)�������� ����e��6��ֱ�������Σ��t�����������w�e��
��
����e��6��ֱ�������Σ��t�����������w�e��
��






 12���O(sh��)
12���O(sh��)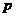 ������(sh��)
������(sh��)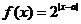 �څ^(q��)�g
�څ^(q��)�g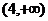 �φ��{(di��o)�f����
�φ��{(di��o)�f����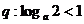 ���������p�����������}����ô��(sh��)��(sh��)
���������p�����������}����ô��(sh��)��(sh��)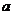 ��ȡֵ������
��
��ȡֵ������
��


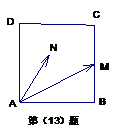 13����D����������
13����D����������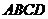 �У���֪
�У���֪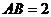 ��
��
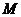 ��
��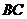 �����c(di��n)����
�����c(di��n)����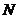 ��������(n��i)����߅�磩����һ�c(di��n)���t
��������(n��i)����߅�磩����һ�c(di��n)���t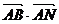 �����ֵ�� ��
�����ֵ�� ��
 14����֪����(sh��)
14����֪����(sh��)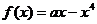 ��
��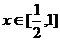 ��
��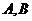 ����D���ϲ�ͬ�ă��c(di��n).��ֱ��
����D���ϲ�ͬ�ă��c(di��n).��ֱ��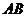 ��б��
���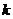 ���M��
���M��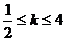 ���t��(sh��)��(sh��)
���t��(sh��)��(sh��) ��ֵ��
��
��ֵ��
��
 ��������}
��������}
 15�������}�M��14�֣�
15�������}�M��14�֣�

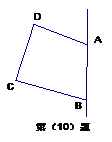
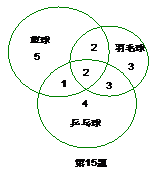 ij�W(xu��)У�@���(du��)����ë���(du��)��ƹ�����(du��)�T��ijЩ�(du��)�T��ֹ������һ֧���(du��)�����w��r��D��ʾ���F(xi��n)�����S�C(j��)��ȡһ���(du��)�T����
ij�W(xu��)У�@���(du��)����ë���(du��)��ƹ�����(du��)�T��ijЩ�(du��)�T��ֹ������һ֧���(du��)�����w��r��D��ʾ���F(xi��n)�����S�C(j��)��ȡһ���(du��)�T����
(1)  ԓ�(du��)�Tֻ����һ֧���(du��)�ĸ��ʣ�
ԓ�(du��)�Tֻ����һ֧���(du��)�ĸ��ʣ�
 ��2��ԓ�(du��)�T������ڃ�֧���(du��)�ĸ���
��2��ԓ�(du��)�T������ڃ�֧���(du��)�ĸ���










 16�������}�M��14�֣���D���������F
16�������}�M��14�֣���D���������F �У�����
�У�����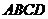 �О����Σ�
�О����Σ�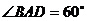 ��
��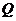 ��
��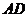 �����c(di��n)��
�����c(di��n)��
��1��  ��
��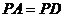 �����C��ƽ��
�����C��ƽ��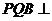 ƽ��
ƽ��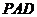 ��
��
��2�� 
 �c(di��n)
�c(di��n)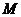 �ھ���
�ھ���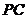 �ϣ�
�ϣ�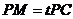 ��ԇ�_����(sh��)��(sh��)
��ԇ�_����(sh��)��(sh��)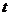 ��ֵ��ʹ��
��ֵ��ʹ��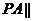 ƽ��
ƽ�� ��
��
17�������}�M��14�֣���֪����(sh��)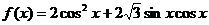 ��
��
��1�� ��(sh��)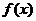 ��
��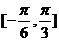 �ϵ�ֵ��
�ϵ�ֵ��
��2�� ��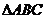 ����
����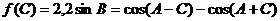 ����
����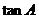 ��ֵ��
��ֵ��
18�������}�M��16�֣���ƽ��ֱ������(bi��o)ϵ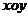 �У���֪���タ
�У���֪���タ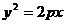 �M����(bi��o)��4���c(di��n)��ԓ���タ�Ľ��c(di��n)�ľ��x��5��
�M����(bi��o)��4���c(di��n)��ԓ���タ�Ľ��c(di��n)�ľ��x��5��
��1�� ���タ�Ę�(bi��o)��(zh��n)���̣�
��2��
�O(sh��)�c(di��n)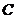 �ǒ��タ�ϵĄ��c(di��n)������
�ǒ��タ�ϵĄ��c(di��n)������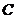 ��A�ĵĈA��
��A�ĵĈA��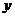 �S�Ͻصõ����L��
�S�Ͻصõ����L��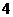 �����C��
�����C��
�A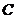 �^���c(di��n)��
�^���c(di��n)��
 19�������}�M��16�֣��O(sh��)
19�������}�M��16�֣��O(sh��)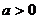 ������(sh��)
������(sh��)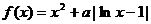 .
.
(1) ��(d��ng)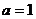 �r(sh��),������
�r(sh��),������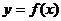 ��
��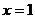 ̎���о�����;
̎���о�����;
(2) ��(d��ng)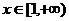 �r(sh��),��(sh��)
�r(sh��),��(sh��)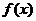 ����Сֵ.
����Сֵ.
20�������}�M��16�֣��ڔ�(sh��)��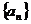 �У���֪
�У���֪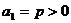 ���ң�
���ң�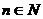
��1�� ����(sh��)��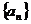 ��Ȳ(sh��)�У���
��Ȳ(sh��)�У���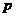 ��ֵ��
��ֵ��
��2�� ��(sh��)��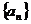 ��ǰ
��ǰ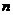 �(xi��ng)��
�(xi��ng)��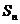
��3�� ��(d��ng)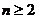 �r(sh��)�����C��
�r(sh��)�����C��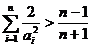
�Ͼ���2009�ø�����һ���{(di��o)��ԇ��(sh��)�W(xu��)�����}
21���x���}(�� ��С�}��ֻ���x��2�}��ÿС�}10��,��Ӌ(j��)2��)
��С�}��ֻ���x��2�}��ÿС�}10��,��Ӌ(j��)2��)
 .�x��
.�x�� �����C���x�v
�����C���x�v
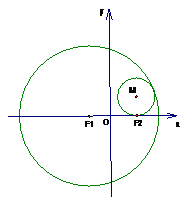
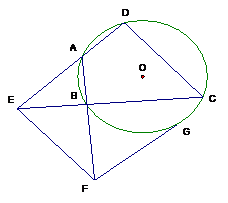 ��D����֪��߅��
��D����֪��߅�� ��(n��i)���ڡ�O,
��(n��i)���ڡ�O,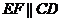 ,
,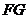 ��O���c(di��n)
��O���c(di��n)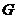 .���C��
.���C��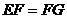 .
.
B.�x��4-2������c׃�Q
��֪���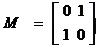 ��
��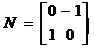 ����ƽ��ֱ������(bi��o)ϵ�У��O(sh��)ֱ��
����ƽ��ֱ������(bi��o)ϵ�У��O(sh��)ֱ��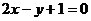 �ھ��
�ھ�� ����(y��ng)��׃�Q�����µõ�������
����(y��ng)��׃�Q�����µõ������� ��������
�������� �ķ��̡�
�ķ��̡�
C.�x��4-4;����(bi��o)ϵ�c����(sh��)����
 ��ֱ֪��
��ֱ֪�� �ͅ���(sh��)���̞�
�ͅ���(sh��)���̞�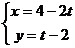
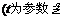 ,
,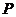 �ǙE�A
�ǙE�A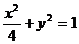 ������һ�c(di��n)�����c(di��n)
������һ�c(di��n)�����c(di��n)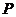 ��ֱ��
��ֱ��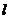 �ľ��x�����ֵ��
�ľ��x�����ֵ��
D���x��4-5������ʽ�x�v
��֪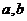 ������(sh��)�����C��
������(sh��)�����C��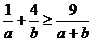 .
.
�����}����22�}����23�}ÿ�}10�֣���20�֡�
22����֪�A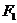 ��
��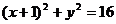 �����c(di��n)���ӈA�^�c(di��n)
�����c(di��n)���ӈA�^�c(di��n) �����c�A
�����c�A ����(n��i)��
����(n��i)��
 ��1�����c(di��n)
��1�����c(di��n)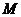 ��܉�E
��܉�E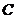 �ķ��̣�
�ķ��̣�
��2�����^ԭ�c(di��n)��ֱ��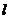 �c��1���е�����
�c��1�������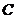 ����
����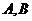 ���c(di��n)����
���c(di��n)����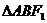 ����e��
����e��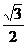 ����ֱ��
����ֱ��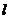 �ķ��̡�
�ķ��̡�
23��֪��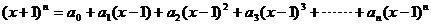
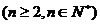
��1����(d��ng)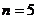 �r(sh��)����
�r(sh��)����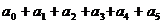 ��ֵ��
��ֵ��
��2���O(sh��)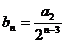 ��
��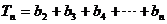 ��ԇ�Ô�(sh��)�W(xu��)�w�{���C����
��ԇ�Ô�(sh��)�W(xu��)�w�{���C����
��(d��ng)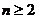 �r(sh��)��
�r(sh��)��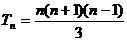
һ�����
1�� ��2��
��2�� ��3��
��3�� ��4��
��4�� ��5��
��5�� ��6��5��7��
��6��5��7�� ��8��
��8�� ��9��
��9�� ��
��
10�� ��11��
��11�� ��12��
��12�� ��13��
��13�� ��14��
��14�� ��
��
��������}
1`5�������}�M��14�֣�
�⣺��1�����O(sh��)��ԓ�(du��)�Tֻ����һ֧���(du��)�ġ����¼�A���t�¼�A�ĸ���

��2���O(sh��)��ԓ�(du��)�T������ڃ�֧���(du��)�ġ����¼�B���t�¼�B�ĸ��ʞ�
�𣺣��ԣ�
16�������}�M��14�֣�
�⣺��1���B ����߅��
����߅�� ����
����  ��
��







 ��
�� �����c(di��n)��
�����c(di��n)�� 
��

 ��
��

 ��2����(d��ng)
��2����(d��ng) �r(sh��)��ʹ��
�r(sh��)��ʹ�� ���B
���B ��
�� ��
�� ����
���� ��
�� ���t
���t ��
�� �����c(di��n)����
�����c(di��n)����
 ��
�� ߅
߅ ���о���
�����
 ����������
���������� �����ģ�������
�����ģ������� ��߅�L��
��߅�L�� ���t
���t ��
�� ��
��




 ����
����
 ��
��
17���⣺
��1��

 ��
��

 �څ^(q��)�g
�څ^(q��)�g �ϵ�ֵ��?y��n)?sub>
�ϵ�ֵ��?y��n)?sub>
��2��
 ��
��


 ��
��




18���⣺��1�����}�⣬�ã� ��
�� ��
��
���タ��(bi��o)��(zh��n)���̞飺
��2���O(sh��)�A�� ������(bi��o)��
������(bi��o)�� ���돽��
���돽�� ��
��

 �A��
�A�� ��
�� �S�Ͻصõ����L��
�S�Ͻصõ����L��


�A�� �ķ��̞飺
�ķ��̞飺
�Ķ�׃?y��u)�?sub> ��
��
��������� �����̢پ�������
�����̢پ�������
���У� ��ã�
��ã�
���ԣ��A �^���c(di��n)��2��0����
�^���c(di��n)��2��0����
19���⣨1����(d��ng) �r(sh��)��
�r(sh��)��
�� ��
��  �������c(di��n)�飨1��2�����о���б�ʞ�1��
�������c(di��n)�飨1��2�����о���б�ʞ�1��
�������� ��
�� ̎���о����̞飺
̎���о����̞飺 ��
��
��2���ٮ�(d��ng) �r(sh��)��
�r(sh��)�� ��
��

 ��
�� �������
�������  ��
�� ��������(sh��)��
��������(sh��)��
�ʮ�(d��ng) �r(sh��)��
�r(sh��)��
�� ��(d��ng) �r(sh��)��
�r(sh��)�� ��
��
 ��
�� ��
��
��i����(d��ng) ��
�� �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)������(sh��)������
�r(sh��)������(sh��)������ �څ^(q��)�g
�څ^(q��)�g �Ϟ�������(sh��)���ʮ�(d��ng)
�Ϟ�������(sh��)���ʮ�(d��ng) �r(sh��)��
�r(sh��)�� ���Ҵ˕r(sh��)
���Ҵ˕r(sh��)
(ii)��(d��ng) ����
���� �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)��ؓ(f��)��(sh��)�����g
�r(sh��)��ؓ(f��)��(sh��)�����g �r(sh��)������(sh��)������
�r(sh��)������(sh��)������ �څ^(q��)�g
�څ^(q��)�g �Ϟ�p����(sh��)����
�Ϟ�p����(sh��)���� �Ϟ�������(sh��)
�Ϟ�������(sh��)
�ʮ�(d��ng) �r(sh��)��
�r(sh��)�� ���Ҵ˕r(sh��)
���Ҵ˕r(sh��)
(iii)��(d��ng) ����
����  �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)��ؓ(f��)��(sh��)������
�r(sh��)��ؓ(f��)��(sh��)������ �څ^(q��)�g[1,e]�Ϟ�p����(sh��)���ʮ�(d��ng)
�څ^(q��)�g[1,e]�Ϟ�p����(sh��)���ʮ�(d��ng) �r(sh��)��
�r(sh��)�� ��
��
�C����������(d��ng) �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)��
�r(sh��)�� �r(sh��)����Сֵ����
�r(sh��)����Сֵ���� ��
��
���Դ˕r(sh��) ����Сֵ��
����Сֵ�� ����(d��ng)
����(d��ng) �r(sh��)��
�r(sh��)�� ��
�� �r(sh��)����Сֵ��
�r(sh��)����Сֵ��
 ����
���� ��
��
���Դ˕r(sh��) ����Сֵ��
����Сֵ�� ��
��
��(d��ng) �r(sh��)����
�r(sh��)���� �r(sh��)��Сֵ��
�r(sh��)��Сֵ�� ����
���� �r(sh��)����Сֵ��
�r(sh��)����Сֵ�� ��
��
�� �����Դ˕r(sh��)
�����Դ˕r(sh��) ����Сֵ��
����Сֵ��
���Ժ���(sh��) ����Сֵ��
����Сֵ��
20���⣺��1���O(sh��)��(sh��)�� �Ĺ����
����� ���t
���t ��
�� ��
��
���}�ã� ����
���� �������
�������
���� ����
���� �������
�������
���� ������
������ ��
��
 ����
���� ��ֵ��2��
��ֵ��2��
��2��

���ԣ�
�� ��(d��ng) ���攵(sh��)����
���攵(sh��)���� �r(sh��)��
�r(sh��)�� ��
��
��˵� ����
����  ��(d��ng)
��(d��ng) Ҳ���ϡ�
Ҳ���ϡ�
�� ��(d��ng) ��ż��(sh��)����
��ż��(sh��)���� �r(sh��)��
�r(sh��)�� ��
�� 
��˵� ����
���� 
 ������
������  �����
�����  ����(d��ng)
����(d��ng) �r(sh��)Ҳ���ϡ�
�r(sh��)Ҳ���ϡ�
���Ԕ�(sh��)�� ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ�� ��
��
��(d��ng) ��ż��(sh��)�r(sh��)��
��ż��(sh��)�r(sh��)��


��(d��ng) ���攵(sh��)�r(sh��)��
���攵(sh��)�r(sh��)�� ��ż��(sh��)��
��ż��(sh��)��


����

�Ͼ���2009�ø�����һ���{(di��o)��ԇ
��(sh��)�W(xu��)�����}������
21���x���}
 .�x��
.�x�� �����C���x�v
�����C���x�v
�C������?y��n)?sub> ��O���c(di��n)
��O���c(di��n) ������
������
��?y��n)?sub> ������
������ 
��A��B��C��D���c(di��n)���A������  ����
���� 
�� ������
������ ��
��
���� ��
��
����  ����
����
B.�x��4-2������c׃�Q
��:���}�O(sh��)�� ,�O(sh��)
,�O(sh��) ��ֱ��
��ֱ�� ������һ�c(di��n),
������һ�c(di��n),
�c(di��n) �ھ��
�ھ�� ����(y��ng)��׃�Q������׃?y��u)?sub>
����(y��ng)��׃�Q������׃?y��u)?sub> ,
,
�t�� , ��
, ��  ,����
,����
��?y��n)��c(di��n) ��ֱ��
��ֱ�� ��,�Ķ�
��,�Ķ� ,����
,����
�������� �ķ��̞�
�ķ��̞� 
C.�x��4-4;����(bi��o)ϵ�c����(sh��)����
�⣺ ֱ�� �ą���(sh��)���̞�
�ą���(sh��)���̞�
 �酢��(sh��)����ֱ��
�酢��(sh��)����ֱ�� ����ͨ���̞�
����ͨ���̞�
��?y��n)?sub> ��E�A
��E�A �������c(di��n)���ʿ��O(sh��)
�������c(di��n)���ʿ��O(sh��) ����
���� ��
��
����c(di��n) ��ֱ��
��ֱ�� �ľ��x��
�ľ��x��
���Ԯ�(d��ng) ��
�� �r(sh��)��
�r(sh��)�� ȡ�����ֵ
ȡ�����ֵ ��
��
D���x��4-5������ʽ�x�v
 �C����
�C���� ������
������ 

�����}����22�}����23�}ÿ�}10�֣���20�֡�
22���⣺��1���O(sh��)�A �İ돽��
�İ돽�� ��
��
��?y��n)�A �c�A
�c�A ������
������
���� ������
������
�����c(di��n) ��܉�E
��܉�E ����
���� �齹�c(di��n)�ęE�A���O(sh��)�E�A���̞�
�齹�c(di��n)�ęE�A���O(sh��)�E�A���̞� ����
����  ������
������
�������� �ķ���
�ķ���
��2����?y��n)�ֱ�� �^�E�A�����ģ��əE�A�Č��Q�Կ�֪��
�^�E�A�����ģ��əE�A�Č��Q�Կ�֪��
��?y��n)?sub> ������
������ ��
��
�����O(sh��)�c(di��n) ��
�� �S�Ϸ����t
�S�Ϸ����t ��
��
���� ��
�� �������c(di��n)
�������c(di��n) ������(bi��o)��
������(bi��o)�� ��
��
����ֱ�� ��б�ʞ�
��б�ʞ� ��������ֱ�����ͳ̞�
��������ֱ�����ͳ̞�
23����1����(d��ng) �r(sh��)��
�r(sh��)��
ԭ��ʽ׃?y��u)?/p>

�� ��
�� 
��2����?y��n)?sub> ����
����

�ٮ�(d��ng) �r(sh��)����߅=
�r(sh��)����߅= ����߅
����߅
��߅=��߅����ʽ������
�ڼ��O(sh��)��(d��ng) �r(sh��)����ʽ��������
�r(sh��)����ʽ��������
����(d��ng) �r(sh��)��
�r(sh��)��
��߅
 ��߅��
��߅��
�ʮ�(d��ng) �r(sh��)����ʽ������
�r(sh��)����ʽ������
�C�Ϣ٢ڣ���(d��ng) �r(sh��)��
�r(sh��)��
www.ks5u.com
 www.ks5u.com
www.ks5u.com
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com