
2008年江西省初中畢業暨中等學校招生考試
數學試卷
說明:本卷共有五個大題, 25個小題;全卷滿分120分;考試時間120分鐘.
一、選擇題(本大題共8小題,每小題3分,共24分);
1.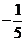 的相反數是( )
的相反數是( )
A.5 B.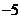 C.
C.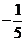 D.
D.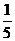
2.不等式組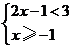 ,的解集是( )
,的解集是( )
A.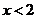 B.
B.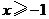 C.
C.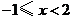 D.無解
D.無解
3.下列四個點,在反比例函數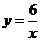 圖象上的是( )
圖象上的是( )
A.(1,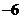 ) B.(2,4) C.(3,
) B.(2,4) C.(3,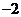 ) D.(
) D.(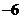 ,
,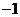 )
)
4.下列四張撲克牌的牌面,不是中心對稱圖形的是( )

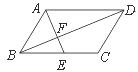
5.如圖,在平行四邊形ABCD中,E是BC的中點,且∠AEC=∠DCE,則下列結論不正確的是( )
A.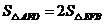 B.
B.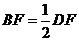
C.四邊形AECD是等腰梯形 D.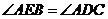
6.在平面直角坐標系中,以點(2,3)為圓心,2為半徑的圓必定( )
A.與 軸相離、與
軸相離、與 軸相切 B.與
軸相切 B.與 軸、
軸、 軸都相離
軸都相離
C.與 軸相切、與
軸相切、與 軸相離 D.與
軸相離 D.與 軸、
軸、 軸都相切
軸都相切
7.下列四個三角形,與右圖中的三角形相似的是( )


8.一個幾何體是由一些大小相同的小正方塊擺成的,其俯視圖與主視圖如圖所示,則組成這個幾何體的小正方塊最多有( )

A.4個 B.5個 C.6個 D.7個
二、填空題(本大題共8小題,每小題3分,共24分)
9.“5?12汶川大地震”發生后,中央電視臺于
10.分解因式: = .
= .
11.將拋物線 向上平移一個單位后,得到的拋物線解析式是 .
向上平移一個單位后,得到的拋物線解析式是 .
12.計算: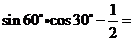 .
.
13.如圖,有一底角為35°的等腰三角形紙片,現過底邊上一點,沿與底邊垂直的方向將其剪開,分成三角形和四邊形兩部分,則四邊形中,最大角的度數是 .
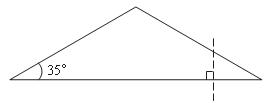
14.方程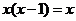 的解是 .
的解是 .
15.某次射擊訓練中,一小組的成績如下表所示:

若該小組的平均成績為7.7環,則成績為8環的人數是 .
16.如圖,已知點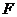 的坐標為(3,0),點
的坐標為(3,0),點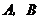 分別是某函數圖象與
分別是某函數圖象與 軸、
軸、 軸的交點,點
軸的交點,點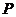 是此圖象上的一動點.設點
是此圖象上的一動點.設點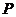 的橫坐標為
的橫坐標為 ,
,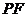 的長為
的長為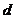 ,且
,且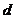 與
與 之間滿足關系:
之間滿足關系: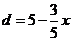 (
(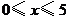 ),給出以下四個結論:①
),給出以下四個結論:①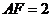 ;②
;②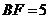 ;③
;③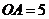 ;④
;④ .其中正確結論的序號是_ .
.其中正確結論的序號是_ .
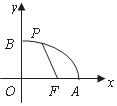
17,先化簡,再求值:
三、(本大題共4小題,每小題4分,共24分)
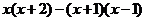 , 其中
, 其中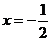 .
.
18.如圖:在平面直角坐標系中,有A(0,1),B( ,0),C(1,0)三點坐標.
,0),C(1,0)三點坐標.
(1)若點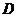 與
與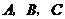 三點構成平行四邊形,請寫出所有符合條件的點
三點構成平行四邊形,請寫出所有符合條件的點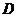 的坐標;
的坐標;
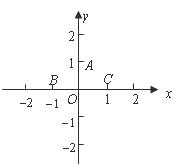
(2)選擇(1)中符合條件的一點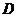 ,求直線
,求直線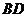 的解析式.
的解析式.
19.有兩個不同形狀的計算器(分別記為A,B)和與之匹配的保護蓋(分別記為a,b)(如圖所示)散亂地放在桌子上.
(1)若從計算器中隨機取一個,再從保護蓋中隨機取一個,求恰好匹配的概率.
(2)若從計算器和保護蓋中隨機取兩個,用樹形圖法或列表法,求恰好匹配的概率.

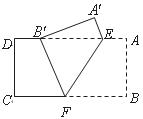
20.如圖,把矩形紙片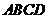 沿
沿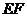 折疊,使點
折疊,使點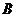 落在邊
落在邊 上的點
上的點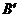 處,點
處,點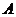 落在點
落在點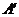 處;
處;
(1)求證: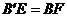 ;
;
(2)設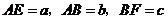 ,試猜想
,試猜想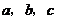 之間的一種關系,并給予證明.
之間的一種關系,并給予證明.
四、(本大題共3小題,每小題8分,共24分)
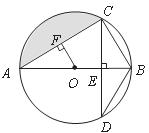
21.如圖,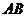 為⊙
為⊙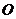 的直徑,
的直徑,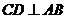 于點
于點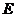 ,交⊙
,交⊙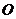 于點
于點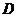 ,
,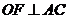 于點
于點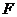 .
.
(1)請寫出三條與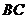 有關的正確結論;
有關的正確結論;
(2)當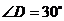 ,
,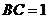 時,求圓中陰影部分的面積.
時,求圓中陰影部分的面積.
22.甲、乙兩同學玩“托球賽跑”游戲,商定:用球拍托著乒乓球從起跑線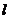 起跑,繞過P點跑回到起跑線(如圖所示);途中乒乓球掉下時須撿起并回到掉球處繼續賽跑,用時少者勝.結果:甲同學由于心急,掉了球,浪費了6秒鐘,乙同學則順利跑完.事后,甲同學說:“我倆所用的全部時間的和為50秒”,乙同學說:“撿球過程不算在內時,甲的速度是我的1.2倍”.根據圖文信息,請問哪位同學獲勝?
起跑,繞過P點跑回到起跑線(如圖所示);途中乒乓球掉下時須撿起并回到掉球處繼續賽跑,用時少者勝.結果:甲同學由于心急,掉了球,浪費了6秒鐘,乙同學則順利跑完.事后,甲同學說:“我倆所用的全部時間的和為50秒”,乙同學說:“撿球過程不算在內時,甲的速度是我的1.2倍”.根據圖文信息,請問哪位同學獲勝?
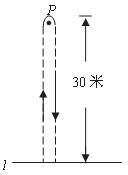
23.為了了解甲、乙兩同學對“字的個數”的估計能力,現場對他們進行了5次測試,測試方法是:拿出一張報紙,隨意用筆畫一個圈,讓他們看了一眼后迅速說出圈內有多少個漢字,但不同的是:甲同學每次估計完字數后不告訴他圈內的實際字數,乙同學每次估計完字數后告訴他圈內的實際字數.根據甲、乙兩同學5次估計情況可繪制統計圖如下:
(1)結合上圖提供的信息,就甲、乙兩同學分別寫出兩條不同類型的正確結論;
(2)若對甲、乙兩同學進行第6次測試,當所圈出的實際字數為100個時,請你用統計知識分別預測他們估計字數的偏差率,并根據預測的偏差率,推算出他們估計的字數所在的范圍.
五、(本大題共2小題,每小題12分,共24分)
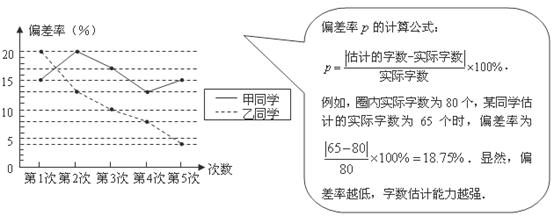
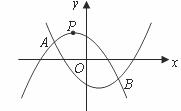
24.如圖,拋物線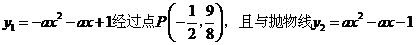 相交于
相交于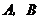 兩點.
兩點.
(1)求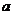 值;
值;
(2)設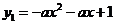 與
與 軸分別交于
軸分別交于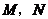 兩點(點
兩點(點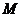 在點
在點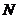 的左邊),
的左邊),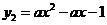 與
與 軸分別交于
軸分別交于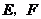 兩點(點
兩點(點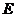 在點
在點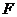 的左邊),觀察
的左邊),觀察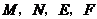 四點的坐標,寫出一條正確的結論,并通過計算說明;
四點的坐標,寫出一條正確的結論,并通過計算說明;
(3)設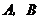 兩點的橫坐標分別記為
兩點的橫坐標分別記為 ,若在
,若在 軸上有一動點
軸上有一動點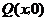 ,且
,且
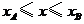 ,過
,過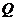 作一條垂直于
作一條垂直于 軸的直線,與兩條拋物線分別交于C,D兩點,試問當
軸的直線,與兩條拋物線分別交于C,D兩點,試問當 為何值時,線段CD有最大值?其最大值為多少?
為何值時,線段CD有最大值?其最大值為多少?
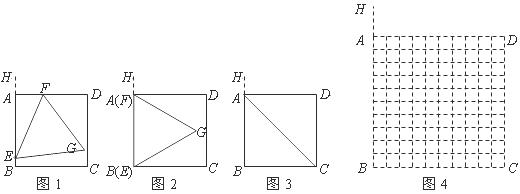
25.如圖1,正方形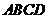 和正三角形
和正三角形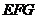 的邊長都為1,點
的邊長都為1,點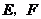 分別在線段
分別在線段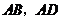 上滑動,設點
上滑動,設點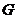 到
到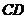 的距離為
的距離為 ,到
,到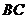 的距離為
的距離為 ,記
,記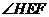 為
為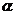 (當點
(當點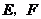 分別與
分別與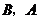 重合時,記
重合時,記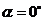 ).
).
(1)當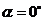 時(如圖2所示),求
時(如圖2所示),求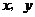 的值(結果保留根號);
的值(結果保留根號);
(2)當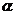 為何值時,點
為何值時,點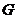 落在對角形
落在對角形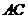 上?請說出你的理由,并求出此時
上?請說出你的理由,并求出此時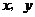 的值(結果保留根號);
的值(結果保留根號);
(3)請你補充完成下表(精確到0.01):
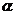
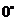
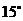
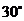
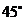
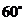
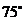
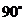

0.03
0
0.29

0.29
0.13
0.03
(4)若將“點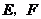 分別在線段
分別在線段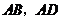 上滑動”改為“點
上滑動”改為“點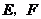 分別在正方形
分別在正方形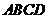 邊上滑動”.當滑動一周時,請使用(3)的結果,在圖4中描出部分點后,勾畫出點
邊上滑動”.當滑動一周時,請使用(3)的結果,在圖4中描出部分點后,勾畫出點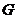 運動所形成的大致圖形.
運動所形成的大致圖形.
(參考數據: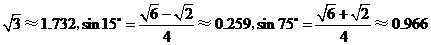 .)
.)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com