
2008年北京市中考試卷分析(數學)
一、選擇題(共8道小題,每小題4分,共32分)
1.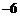 的絕對值等于( )
的絕對值等于( )
A.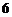 B.
B.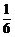 C.
C.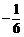 D.
D.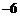
2.截止到
A.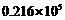 B.
B.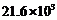 C.
C.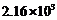 D.
D.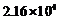
3.若兩圓的半徑分別是
A.內切 B.相交 C.外切 D.外離
4.眾志成城,抗震救災.某小組7名同學積極捐出自己的零花錢支援災區,他們捐款的數額分別是(單位:元):50,20,50,30,50,25,135.這組數據的眾數和中位數分別是( )
A.50,20 B.50,
5.若一個多邊形的內角和等于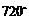 ,則這個多邊形的邊數是( )
,則這個多邊形的邊數是( )
A.5 B.6 C.7 D.8
6.如圖,有5張形狀、大小、質地均相同的卡片,正面分別印有北京奧運會的會徽、吉祥物(福娃)、火炬和獎牌等四種不同的圖案,背面完全相同.現將這5張卡片洗勻后正面向下放在桌子上,從中隨機抽取一張,抽出的卡片正面圖案恰好是吉祥物(福娃)的概率是( )

A.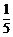 B.
B.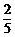 C.
C.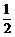 D.
D.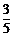
7.若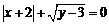 ,則
,則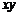 的值為( )
的值為( )
A.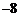 B.
B.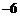 C.
C. D.
D.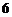
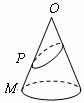
8.已知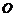 為圓錐的頂點,
為圓錐的頂點,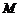 為圓錐底面上一點,點
為圓錐底面上一點,點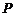 在
在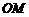 上.一只蝸牛從
上.一只蝸牛從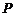 點出發,繞圓錐側面爬行,回到
點出發,繞圓錐側面爬行,回到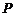 點時所爬過的最短路線的痕跡如右圖所示.若沿
點時所爬過的最短路線的痕跡如右圖所示.若沿 將圓錐側面剪開并展開,所得側面展開圖是( )
將圓錐側面剪開并展開,所得側面展開圖是( )
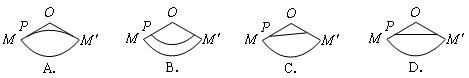
二、填空題(共4道小題,每小題4分,共16分)
9.在函數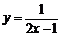 中,自變量
中,自變量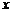 的取值范圍是
.
的取值范圍是
.
10.分解因式: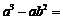 .
.
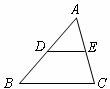
11.如圖,在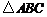 中,
中,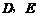 分別是
分別是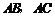 的中點,若
的中點,若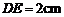 ,則
,則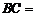 cm.
cm.
12.一組按規律排列的式子: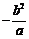 ,
,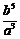 ,
,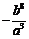 ,
,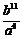 ,…(
,…(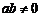 ),其中第7個式子是 ,第
),其中第7個式子是 ,第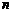 個式子是 (
個式子是 (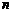 為正整數).
為正整數).
三、解答題(共5道小題,共25分)
13.(本小題滿分5分)
計算: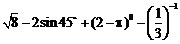 .
.
14.(本小題滿分5分)
解不等式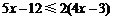 ,并把它的解集在數軸上表示出來.
,并把它的解集在數軸上表示出來.
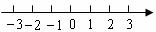
15.(本小題滿分5分)
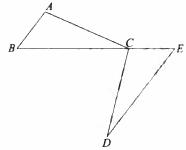
已知:如圖,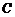 為
為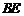 上一點,點
上一點,點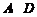 分別在
分別在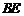 兩側.
兩側.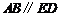 ,
,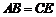 ,
,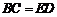 .求證:
.求證: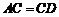 .
.
16.(本小題滿分5分)
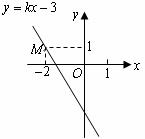
如圖,已知直線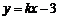 經過點
經過點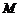 ,求此直線與
,求此直線與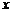 軸,
軸,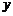 軸的交點坐標.
軸的交點坐標.
17.(本小題滿分5分)
已知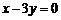 ,求
,求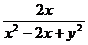 的值.
的值.
四、解答題(共2道小題,共10分)
18.(本小題滿分5分)
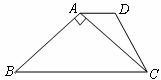
如圖,在梯形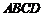 中,
中,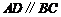 ,
,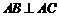 ,
,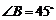 ,
,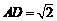 ,
,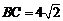 ,求
,求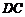 的長.
的長.
19.(本小題滿分5分)
已知:如圖,在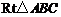 中,
中,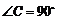 ,點
,點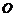 在
在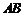 上,以
上,以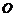 為圓心,
為圓心,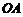 長為半徑的圓與
長為半徑的圓與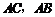 分別交于點
分別交于點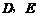 ,且
,且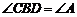 .
.
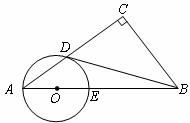
(1)判斷直線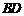 與⊙O的位置關系,并證明你的結論;
與⊙O的位置關系,并證明你的結論;
(2)若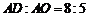 ,
,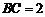 ,求
,求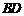 的長.
的長.
五、解答題(本題滿分6分)
20.為減少環境污染,自2008年6月1日起,全國的商品零售場所開始實行“塑料購物袋有償使用制度”(以下簡稱“限塑令”).某班同學于6月上旬的一天,在某超市門口采用問卷調查的方式,隨機調查了“限塑令”實施前后,顧客在該超市用購物袋的情況,以下是根據100位顧客的100份有效答卷畫出的統計圖表的一部分:
“限塑令”實施后,塑料購物袋使用后的處理方式統計表
處理方式
直接丟棄
直接做垃圾袋
再次購物使用
其它
選該項的人數占
總人數的百分比
5%
35%
49%
11%
請你根據以上信息解答下列問題:
(1)補全圖1,“限塑令”實施前,如果每天約有2000人次到該超市購物.根據這100位顧客平均一次購物使用塑料購物袋的平均數,估計這個超市每天需要為顧客提供多少個塑料購物袋?
(2)補全圖2,并根據統計圖和統計表說明,購物時怎樣選用購物袋,塑料購物袋使用后怎樣處理,能對環境保護帶來積極的影響.
六、解答題(共2道小題,共9分)
21.(本小題滿分5分)列方程或方程組解應用題:
京津城際鐵路將于2008年8月1日開通運營,預計高速列車在北京、天津間單程直達運行時間為半小時.某次試車時,試驗列車由北京到天津的行駛時間比預計時間多用了6分鐘,由天津返回北京的行駛時間與預計時間相同.如果這次試車時,由天津返回北京比去天津時平均每小時多行駛40千米,那么這次試車時由北京到天津的平均速度是每小時多少千米?
22.(本小題滿分4分)
已知等邊三角形紙片 的邊長為
的邊長為 ,
, 為
為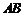 邊上的點,過點
邊上的點,過點 作
作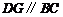 交
交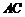 于點
于點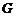 .
.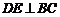 于點
于點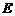 ,過點
,過點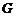 作
作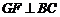 于點
于點 ,把三角形紙片
,把三角形紙片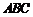 分別沿
分別沿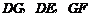 按圖1所示方式折疊,點
按圖1所示方式折疊,點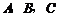 分別落在點
分別落在點 ,
,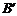 ,
,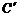 處.若點
處.若點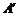 ,
,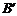 ,
,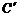 在矩形
在矩形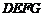 內或其邊上,且互不重合,此時我們稱
內或其邊上,且互不重合,此時我們稱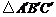 (即圖中陰影部分)為“重疊三角形”.
(即圖中陰影部分)為“重疊三角形”.
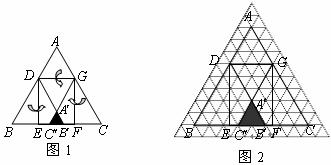
(1)若把三角形紙片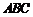 放在等邊三角形網格中(圖中每個小三角形都是邊長為1的等邊三角形),點
放在等邊三角形網格中(圖中每個小三角形都是邊長為1的等邊三角形),點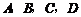 恰好落在網格圖中的格點上.如圖2所示,請直接寫出此時重疊三角形
恰好落在網格圖中的格點上.如圖2所示,請直接寫出此時重疊三角形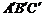 的面積;
的面積;
(2)實驗探究:設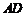 的長為
的長為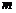 ,若重疊三角形
,若重疊三角形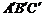 存在.試用含
存在.試用含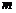 的代數式表示重疊三角形
的代數式表示重疊三角形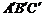 的面積,并寫出
的面積,并寫出 的取值范圍(直接寫出結果,備用圖供實驗,探究使用).
的取值范圍(直接寫出結果,備用圖供實驗,探究使用).
七、解答題(本題滿分7分)
23.已知:關于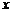 的一元二次方程
的一元二次方程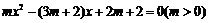 .
.
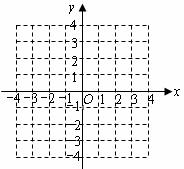
(1)求證:方程有兩個不相等的實數根;
(2)設方程的兩個實數根分別為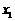 ,
,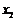 (其中
(其中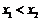 ).若
).若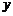 是關于
是關于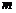 的函數,且
的函數,且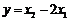 ,求這個函數的解析式;
,求這個函數的解析式;
(3)在(2)的條件下,結合函數的圖象回答:當自變量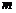 的取值范圍滿足什么條件時,
的取值范圍滿足什么條件時,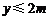 .
.
八、解答題(本題滿分7分)
24.在平面直角坐標系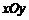 中,拋物線
中,拋物線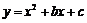 與
與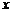 軸交于
軸交于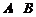 兩點(點
兩點(點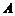 在點
在點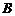 的左側),與
的左側),與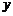 軸交于點
軸交于點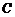 ,點
,點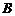 的坐標為
的坐標為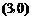 ,將直線
,將直線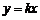 沿
沿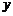 軸向上平移3個單位長度后恰好經過
軸向上平移3個單位長度后恰好經過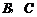 兩點.
兩點.
(1)求直線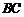 及拋物線的解析式;
及拋物線的解析式;
(2)設拋物線的頂點為 ,點
,點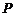 在拋物線的對稱軸上,且
在拋物線的對稱軸上,且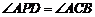 ,求點
,求點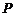 的坐標;
的坐標;
(3)連結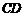 ,求
,求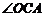 與
與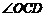 兩角和的度數.
兩角和的度數.
九、解答題(本題滿分8分)
問題:如圖1,在菱形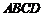 和菱形
和菱形 中,點
中,點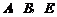 在同一條直線上,
在同一條直線上,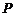 是線段
是線段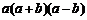 的中點,連結
的中點,連結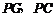 .若
.若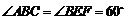 ,探究
,探究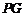 與
與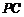 的位置關系及
的位置關系及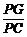 的值.
的值.
小聰同學的思路是:延長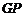 交
交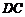 于點
于點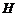 ,構造全等三角形,經過推理使問題得到解決.
,構造全等三角形,經過推理使問題得到解決.
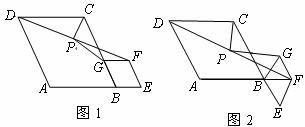
請你參考小聰同學的思路,探究并解決下列問題:
(1)寫出上面問題中線段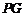 與
與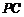 的位置關系及
的位置關系及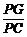 的值;
的值;
(2)將圖1中的菱形 繞點
繞點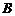 順時針旋轉,使菱形
順時針旋轉,使菱形 的對角線
的對角線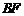 恰好與菱形
恰好與菱形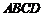 的邊
的邊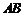 在同一條直線上,原問題中的其他條件不變(如圖2).你在(1)中得到的兩個結論是否發生變化?寫出你的猜想并加以證明.
在同一條直線上,原問題中的其他條件不變(如圖2).你在(1)中得到的兩個結論是否發生變化?寫出你的猜想并加以證明.
(3)若圖1中 ,將菱形
,將菱形 繞點
繞點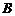 順時針旋轉任意角度,原問題中的其他條件不變,請你直接寫出
順時針旋轉任意角度,原問題中的其他條件不變,請你直接寫出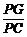 的值(用含
的值(用含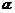 的式子表示).
的式子表示).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com