
題目列表(包括答案和解析)
17.證明:假設f(x)至少有兩個零點。不妨設有兩個零點![]() 與
與![]() ,則f(
,則f(![]() )=0,f(
)=0,f(![]() )=0
)=0
所以f(![]() )=f(
)=f(![]() )與已知f(x)是單調函數矛盾,所以假設錯誤,因此f(x)在其定義域上是單調函數證明f(x)至多有一個零點
)與已知f(x)是單調函數矛盾,所以假設錯誤,因此f(x)在其定義域上是單調函數證明f(x)至多有一個零點
一批產品共10件,其中7件正品,3件次品,每次從這批產品中任取一件,在下述三種情況下,分別求直至取得正品時所需次數X的概率分布。
(1)每次取出的產品不再放回去;
(2)每次取出的產品仍放回去;
(3)每次取出一件次品后,總是另取一件正品放回到這批產品中.
某射手每次射擊擊中目標的概率是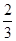 ,且各次射擊的結果互不影響。
,且各次射擊的結果互不影響。
(Ⅰ)假設這名射手射擊5次,求恰有2次擊中目標的概率
(Ⅱ)假設這名射手射擊5次,求有3次連續擊中目標。另外2次未擊中目標的概率;
(Ⅲ)假設這名射手射擊3次,每次射擊,擊中目標得1分,未擊中目標得0分,在3次射擊中,若有2次連續擊中,而另外1次未擊中,則額外加1分;若3次全擊中,則額外加3分,記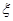 為射手射擊3次后的總的分數,求
為射手射擊3次后的總的分數,求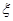 的分布列。
的分布列。
某射手每次射擊擊中目標的概率是 ,且各次射擊的結果互不影響。
,且各次射擊的結果互不影響。
(Ⅰ)假設這名射手射擊5次,求恰有2次擊中目標的概率
(Ⅱ)假設這名射手射擊5次,求有3次連續擊中目標。另外2次未擊中目標的概率;
(Ⅲ)假設這名射手射擊3次,每次射擊,擊中目標得1分,未擊中目標得0分,在3次射擊中,若有2次連續擊中,而另外1次未擊中,則額外加1分;若3次全擊中,則額外加3分,記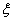 為射手射擊3次后的總的分數,求
為射手射擊3次后的總的分數,求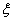 的分布列。
的分布列。
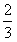 ,且各次回答問題的結果互不影響。
,且各次回答問題的結果互不影響。
現有甲、乙兩個項目。對甲項目每投資十萬元,一年后利潤是1.2萬元、1.18萬元、1.17萬元的概率分別為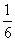 、
、 、
、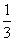 ;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是
;已知乙項目的利潤與產品價格的調整有關,在每次調整中價格下降的概率都是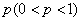 。設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為
。設乙項目產品價格在一年內進行2次獨立的調整,記乙項目產品價格在一年內的下降次數為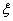 。對乙項目每投資十萬元,
。對乙項目每投資十萬元, 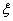 取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元。隨機變量
取0、1、2時,一年后相應利潤是1.3萬元、1.25萬元、0.2萬元。隨機變量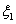 、
、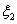 分別表示對甲、乙兩項目各投資十萬元一年后的利潤。
分別表示對甲、乙兩項目各投資十萬元一年后的利潤。
(I) 求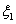 、
、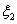 的概率分布和數學期望
的概率分布和數學期望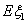 、
、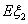 ;
;
(II) 當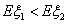 時,求
時,求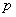 的取值范圍。
的取值范圍。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com