
題目列表(包括答案和解析)
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 5 |
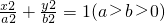 的離心率e為
的離心率e為 ,且橢圓C的一個焦點與拋物線y2=-12x的焦點重合.
,且橢圓C的一個焦點與拋物線y2=-12x的焦點重合.設橢圓 (常數
(常數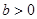 )的左右焦點分別為
)的左右焦點分別為 ,
, 是直線
是直線 上的兩個動點,
上的兩個動點, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一問中解:設 ,
, 則
則
由 得
得 由
由 ,得
,得
 ②
②

第二問易求橢圓 的標準方程為:
的標準方程為:
 ,
,
所以,當且僅當 或
或 時,
時, 取最小值
取最小值 .
.
解:設 ,
, ……………………1分
……………………1分
則 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求橢圓 的標準方程為:
的標準方程為: .………………2分
.………………2分
 , ……4分
, ……4分
所以,當且僅當 或
或 時,
時, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,當且僅當 或
或 時,
時, 取最小值
取最小值
已知A、D分別為橢圓E:  的左頂點與上頂點,橢圓的離心率
的左頂點與上頂點,橢圓的離心率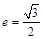 ,F1、F2為橢圓的左、右焦點,點P是線段AD上的任一點,且
,F1、F2為橢圓的左、右焦點,點P是線段AD上的任一點,且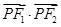 的最大值為1 .
的最大值為1 .
(1)求橢圓E的方程;
(2)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且OA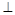 OB(O為坐標原點),若存在,求出該圓的方程;若不存在,請說明理由;
OB(O為坐標原點),若存在,求出該圓的方程;若不存在,請說明理由;
(3)設直線l與圓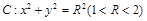 相切于A1,且l與橢圓E有且僅有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
相切于A1,且l與橢圓E有且僅有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
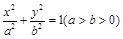 的左頂點與上頂點,橢圓的離心率
的左頂點與上頂點,橢圓的離心率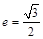 ,F1、F2為橢圓的左、右焦點,點P是線段AD上的任一點,且
,F1、F2為橢圓的左、右焦點,點P是線段AD上的任一點,且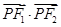 的最大值為1 .
的最大值為1 .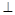 OB(O為坐標原點),若存在,求出該圓的方程;若不存在,請說明理由;
OB(O為坐標原點),若存在,求出該圓的方程;若不存在,請說明理由;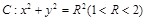 相切于A1,且l與橢圓E有且僅有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
相切于A1,且l與橢圓E有且僅有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.1. {2,8} 2.  3.
3.  4.
4. 
5. 
 6. 1 7.20
6. 1 7.20
8.  9.
9.  10.2
10.2
11. 12.
12.  13. [2,3] 14.
13. [2,3] 14. 
15.證明:(Ⅰ)在 中,
中,
∵ ,
, ,
, ,∴
,∴ .
.
∴ .????????????????? 2分
.????????????????? 2分
又 ∵平面 平面
平面 ,
,
平面 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 .
.
又 平面
平面 ,
,
∴平面 平面
平面 .………………………………………………………………4分
.………………………………………………………………4分
(Ⅱ)當 點位于線段PC靠近C點的三等分點處時,
點位于線段PC靠近C點的三等分點處時, 平面
平面 .………5分
.………5分
證明如下:連接AC,交 于點N,連接MN.
于點N,連接MN.
∵ ,所以四邊形
,所以四邊形 是梯形.
是梯形.
∵ ,∴
,∴ .
.
又 ∵ ,
,
∴
 ,∴
,∴ MN.…………………………………………………7分
MN.…………………………………………………7分
∵ 平面
平面 ,∴
,∴ 平面
平面 .………………………………………9分
.………………………………………9分
(Ⅲ)過 作
作 交
交 于
于 ,
,
∵平面 平面
平面 ,
,
∴ 平面
平面 .
.
即 為四棱錐
為四棱錐 的高.……………………………………………………11分
的高.……………………………………………………11分
又 ∵ 是邊長為4的等邊三角形,∴
是邊長為4的等邊三角形,∴ .……………12分
.……………12分
 在
在 中,斜邊
中,斜邊 邊上的高為
邊上的高為 ,此即為梯形
,此即為梯形 的高.
的高.
∴梯形 的面積
的面積 .
.
故 .……………………………………………14分
.……………………………………………14分
16.設 的二次項系數為
的二次項系數為 ,其圖象上兩點為(
,其圖象上兩點為( ,
, )、B(
)、B( ,
, )因為
)因為 ,
, ,所以
,所以 ,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
,由x的任意性得f(x)的圖象關于直線x=1對稱, ………………………………………………………………(2分)
∵  ,
, ,
, ,
,
 ,
, ,
,
 ,………………………………(4分)
,………………………………(4分)
∴ 當 時,∵f(x)在x≥1內是增函數,
時,∵f(x)在x≥1內是增函數,





 ,
, .
.
∵  , ∴
, ∴  .………………………………………………(8分)
.………………………………………………(8分)
當 時,∵f(x)在x≥1內是減函數.
時,∵f(x)在x≥1內是減函數.
同理可得 或
或 ,
, .………………………………………(11分)
.………………………………………(11分)
綜上: 的解集是當
的解集是當 時,為
時,為
當 時,為
時,為 ,或
,或 .
.
17.解:(1)若 千米/小時,每小時耗油量為
千米/小時,每小時耗油量為 升/小時. 共耗油
升/小時. 共耗油 升.
升.
所以,從甲地到乙地要耗油
(2)設當汽車以 千米/小時的速度勻速行駛時耗油量最少,
千米/小時的速度勻速行駛時耗油量最少, ,耗油量為S升.
,耗油量為S升.
則 ,
,
 ,
,
令 ,解得,
,解得, .
.
列表:











單調減
極小值11.25
單調增

所以,當汽車以
18.解:(Ⅰ)設

對稱軸方程 ,由題意
,由題意 或
或 或
或
∴ 或
或 或
或 ∴
∴
(Ⅱ)由已知與(Ⅰ)得: ,
, ,
,
 ,
, ,
, .
.
 橢圓的標準方程為
橢圓的標準方程為 .
.
設 ,
, ,聯立
,聯立
得 ,
,

又 ,
,
因為橢圓的右頂點為 ,
, ,即
,即 ,
,
 ,
,
 ,
, .
.
解得: ,
, ,且均滿足
,且均滿足 ,
,
當 時,
時, 的方程為
的方程為 ,直線過定點
,直線過定點 ,與已知矛盾;
,與已知矛盾;
當 時,
時, 的方程為
的方程為 ,直線過定點
,直線過定點 .
.
所以,直線 過定點,定點坐標為
過定點,定點坐標為 .
.
19. 解: (1) 由題知:  , 解得
, 解得 , 故
, 故 .
.
(2)  ,
,
 ,
,
 ,
,
又 滿足上式. 所以
滿足上式. 所以 .
.
(3) 若 是
是 與
與 的等差中項, 則
的等差中項, 則 ,
,
從而 , 得
, 得 .
.
因為 是
是 的減函數, 所以
的減函數, 所以
當 , 即
, 即 時,
時,  隨
隨 的增大而減小, 此時最小值為
的增大而減小, 此時最小值為 ;
;
當 , 即
, 即 時,
時,  隨
隨 的增大而增大, 此時最小值為
的增大而增大, 此時最小值為 .
.
又 , 所以
, 所以 ,
,
即數列 中
中 最小, 且
最小, 且 .
.
20. 解:(1)由題意得

而 ,所以
,所以 、
、 的關系為
的關系為
(2)由(1)知 ,
,

令 ,要使
,要使 在其定義域
在其定義域 內是單調函數,只需
內是單調函數,只需 在
在 內滿足:
內滿足: 恒成立.
恒成立.
①當 時,
時, ,因為
,因為 >
> ,所以
,所以 <0,
<0, <0,
<0,
∴ 在
在 內是單調遞減函數,即
內是單調遞減函數,即 適合題意;
適合題意;
②當 >0時,
>0時, ,其圖像為開口向上的拋物線,對稱軸為
,其圖像為開口向上的拋物線,對稱軸為 ,∴
,∴ ,
,
只需 ,即
,即 ,
,
∴ 在
在 內為單調遞增函數,故
內為單調遞增函數,故 適合題意.
適合題意.
③當 <0時,
<0時, ,其圖像為開口向下的拋物線,對稱軸為
,其圖像為開口向下的拋物線,對稱軸為 ,只要
,只要 ,即
,即 時,
時, 在
在 恒成立,故
恒成立,故 <0適合題意.
<0適合題意.
綜上所述, 的取值范圍為
的取值范圍為 .
.
(3)∵ 在
在 上是減函數,
上是減函數,
∴ 時,
時, ;
; 時,
時, ,即
,即 ,
,
①當 時,由(2)知
時,由(2)知 在
在 上遞減
上遞減 <2,不合題意;
<2,不合題意;
②當0< <1時,由
<1時,由 ,
,
又由(2)知當 時,
時, 在
在 上是增函數,
上是增函數,
∴ <
< ,不合題意;
,不合題意;
③當 時,由(2)知
時,由(2)知 在
在 上是增函數,
上是增函數, <2,又
<2,又 在
在 上是減函數,
上是減函數,
故只需 >
> ,
, ,而
,而 ,
,
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com