題目列表(包括答案和解析)
極值的求法
若x是點x0附近的任一點，當x＜x0時
(x)＞0且當x＞x0時(x)＜0，則f(x0)是f(x)的一個________；當x＜x0時(x)＜0且當x＞x0時(x)＞0，則f(x0)是f(x)的一個________．
| 3 |
| 3 |
設
的極小值為
,其導函數
的圖像經過點
,如圖所示,
（1）求
的解析式；
（2）若對
都有
恒成立，
求實數
的取值范圍。
。
（Ⅰ）求
的極值點；
（Ⅱ）當
時，若方程
在
上有兩個實數解，求實數t的取值范圍；
(Ⅲ）證明：當
時，
。
（10分）設函數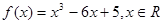
.
⑴ 求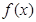
的極值點；
⑵ 若關于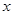
的方程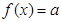
有3個不同實根，求實數a的取值范圍.
⑶ 已知當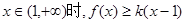
恒成立，求實數k的取值范圍.
一、選擇題: B A B D A B D C B D Ｂ Ｃ
二、填空題： 13.
14．－８
15．1 16．①②
三、解答題：
18．解：依題意，第四項指標抽檢合格的概率為 
其它三項指標抽檢合格的概率均為
。
（1）若食品監管部門對其四項質量指標依次進行嚴格的檢測，恰好在第三項指標檢測結束時， 能確定該食品不能上市的概率等于第一、第二項指標中恰有一項不合格而且第三項指標不合格的概率．
(2)該品牌的食品能上市的概率等于四項指標都含格或第一、第二、第三項指標中僅有
一項不合格且第四項指標合格的概率．
故二面角
的大小為
解法二：如圖，以
為原點，建立空間直角坐標系，使
軸，
、
分別在
軸、
軸上。
（1）由已知，
，
，
，
，
，
，
∴
， 
，
，
∵
， ∴
，
又
，∴
21.解：（1）設直線
的方程為
，聯立，得
由△
得,
或
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com