
【題目】綜合與探究
問題情境:
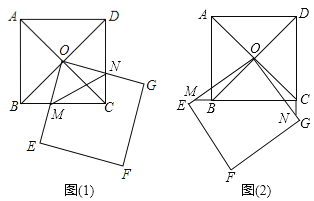
在綜合實踐課上,李老師讓同學們根據如下問題情境,寫出兩個數學結論:如圖(1),正方形ABCD的對角線交于點O,點O又是正方形OEFG的一個頂點(正方形OEFG的邊長足夠長),將正方形OEFG繞點O做旋轉實驗,OE與BC交于點M,OG與DC交于點N.
“興趣小組”寫出的兩個數學結論是:
①S△OMC+S△ONC=![]() S正方形ABCD;
S正方形ABCD;
②BM2+CM2=2OM2.
問題解決:
(1)請你證明“興趣小組”所寫的兩個結論的正確性.
類比探究:
(2)解決完“興趣小組”的兩個問題后,老師讓同學們繼續探究,再提出新的問題;“智慧小組“提出的問題是:如圖(2),將正方形OEFG在圖(1)的基礎上旋轉一定的角度,當OE與CB的延長線交于點M,OG與DC的延長線交于點N,則“興趣小組”所寫的兩個結論是否仍然成立?請說明理由.
【答案】(1)詳見解析;(2)結論①不成立,結論②成立,理由詳見解析.
【解析】
(1)①利用正方形的性質判斷出△BOM≌△CON,利用面積和差即可得出結論;
②先得出OM=ON,BM=CN,再用勾股定理即可得出結論;
(2)同(1)的方法即可得出結論.
解:(1)①∵正方形ABCD的對角線相交于O,
∴S△BOC=![]() S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
S正方形ABCD,OB=OC,∠BOC=90°,∠OBM=∠OCN,
∵四邊形OEFG是正方形,
∴∠MON=90°,
∴∠BOC﹣∠MOC=∠MON﹣∠MOC,
∴∠BOM=∠COM,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC+S△ONC=S△OMC+S△BOM=![]() S正方形ABCD;
S正方形ABCD;
②由①知,△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2;
(2)結論①不成立,
理由:∵正方形ABCD的對角線相交于O,
∴S△BOC=![]() S正方形ABCD,OB=
S正方形ABCD,OB=![]() BD,OC=
BD,OC=![]() AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
AC,AC=BD,AC⊥BD,∠ABC=∠BCD=90°,AC平分∠BCD,BD平分∠ABC,
∴OB=OC,∠BOC=90°,∠OBC=∠OCD=45°,
∴∠OBM=∠OCN=135°,
∵四邊形OEFG是正方形,
∴∠MON=90°,
∴∠BOM=∠CON,
∴△BOM≌△CON,
∴S△BOM=S△CON,
∴S△OMC﹣S△BOM=S△OMC﹣S△CON=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴結論①不成立;
結論②成立,理由:
如圖(2)
連接MN,∵△BOM≌△CON,
∴OM=ON,BM=CN,
在Rt△MCN中,MN2=CM2+CN2=CM2+BM2,
在Rt△MON中,MN2=OM2+ON2=2OM2,
∴BM2+CM2=2OM2,
∴結論②成立.


科目:初中數學 來源: 題型:
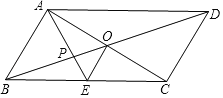
【題目】如圖,平行四邊形ABCD的對角線AC、BD相交于點O,AE平分∠BAD,分別交BC、BD于點E、P,連接OE,∠ADC=60°,AB=![]() BC=1,則下列結論:
BC=1,則下列結論:
①∠CAD=30°②BD=![]() ③S平行四邊形ABCD=ABAC④OE=
③S平行四邊形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正確的個數是( )
,正確的個數是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有甲、乙兩個不透明的布袋,甲袋中有兩個完全相同的小球,分別標有數字1和-2;乙袋中有三個完全相同的小球,分別標有數字-1、0和2.小麗先從甲袋中隨機取出一個小球,記錄下小球上的數字為x;再從乙袋中隨機取出一個小球,記錄下小球上的數字為y,設點A的坐標為(x,y).
(1)請用表格或樹狀圖列出點A所有可能的坐標;
(2)求點A在反比例函數y=![]() 圖象上的概率.
圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市居民使用自來水按月收費,標準如下:
①若每戶月用水不超過![]() ,按
,按![]() 元/
元/![]() 收費;
收費;
②若超過![]() ,但不超過
,但不超過![]() ,則超過的部分按
,則超過的部分按![]() 元/
元/![]() 收費,未超過
收費,未超過![]() 部分按①標準收費;
部分按①標準收費;
③若超過![]() ,超過的部分按
,超過的部分按![]() 元/
元/![]() 收費,未超過
收費,未超過![]() 部分按②標準收費;
部分按②標準收費;
(1)若用水![]() ,應交水費______元;(用含
,應交水費______元;(用含![]() 的式子表示)
的式子表示)
(2)小明家上個月用水![]() ,交水費
,交水費![]() 元,求
元,求![]() 的值;
的值;
(3)在(2)的條件下,小明家七、八兩個月共交水費![]() 元,七月份用水
元,七月份用水![]() 超過
超過![]() ,但不足
,但不足![]() ,八月份用水
,八月份用水![]() 超過
超過![]() ,當
,當![]() 均為整數時,求
均為整數時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】多邊形上或內部的一點與多邊形各頂點的連線,可以將多邊形分割成若干個小三角形.如圖,給出了四邊形的三種具體分割方法,分別將四邊形分割成了2個、3個、4個小三角形,這樣我們就可以借助研究三角形的經驗研究四邊形了.
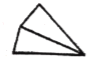
圖①被分割成2個小三角形

圖②被分割成3個小三角形

圖③被分割成4個小三角形
(1)請按照上述三種方法分別將圖中的六邊形進行分割,并寫出每種方法所得到的小三角形的個數:
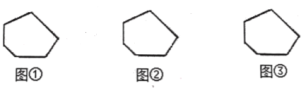
圖①被分割成 個小三角形、圖②被分割成 個小三角形、圖③被分割成 個小三角形;
(2)如果按照上述三種分割方法分別分割![]() 邊形,請寫出每種方法所得到的小三角形的個數(用含
邊形,請寫出每種方法所得到的小三角形的個數(用含![]() 的代數式寫出結論即可,不必畫圖):按照上述圖①、圖②、圖③的分割方法,
的代數式寫出結論即可,不必畫圖):按照上述圖①、圖②、圖③的分割方法,![]() 邊形分別可以被分割成 、 、 個小三角形.
邊形分別可以被分割成 、 、 個小三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列![]() 個生產、生活現象中,可用“兩點之間線段最短”來解釋的是( )
個生產、生活現象中,可用“兩點之間線段最短”來解釋的是( )
A.用兩根釘子就可以把木條固定在墻上
B.植樹時,只要選出兩棵樹的位置,就能確定同一行樹所在的直線
C.把彎曲的公路改直,就能縮短路程
D.砌墻時,經常在兩個墻角的位置分別插一根木樁拉一條直的參照線
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點![]() 在直線
在直線![]() 上,在直線
上,在直線![]() 的同側,作射線
的同側,作射線![]() 平分
平分![]() .
.
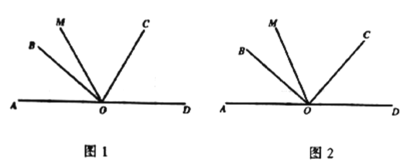
(1)如圖1,若![]() ,
,![]() ,直接寫出
,直接寫出![]() 的度數為 ,
的度數為 ,![]() 的度數為 ;
的度數為 ;
(2)如圖2,若![]() ,求
,求![]() 的度數;
的度數;
(3)若![]() 和
和![]() 互為余角且
互為余角且![]() ,
,![]() 平分
平分![]() ,試畫出圖形探究
,試畫出圖形探究![]() 與
與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com