
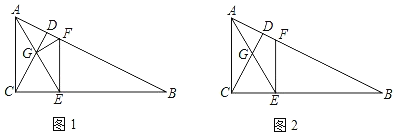
【題目】如圖1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E為線段BC上一點,AE交CD于G,且GC=GE,EF⊥BC交AB于點F.
(1)求證:AE2=AFAB;
(2)連FG,若BE=2CE,求tan∠AFG;
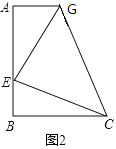
(3)如圖2,當tanB= 時,CE=FE(請直接寫出結果,不需要解答過程).
【答案】(1)證明見解析;(2)tan∠AFG=![]() ;(3)
;(3)![]() .
.
【解析】
(1)先證明∠AEF=∠B,然后再證明△AEF∽△ABE,最后根據相似三角形的性質即可證明;
(2)設CE=a.則BE=2a,證明△AEC∽△BAC,得到AC=![]() a,易得∠AFG=60°,最后根據特殊角的三角函數值求解即可;
a,易得∠AFG=60°,最后根據特殊角的三角函數值求解即可;
(3)設BE=a,CE=EF=b,證明 △AEC∽△BAC.得到AC=![]() ,證明△BEF∽△BCA得到a、b的關系,最后根據正切的定義解答即可.
,證明△BEF∽△BCA得到a、b的關系,最后根據正切的定義解答即可.
(1)證明:∵GC=GE,
∴∠GCE=∠GEC,
∵CD⊥AB,
∴∠DCE+∠B=90°,
∵EF⊥BC,
∴∠GEC+∠AEF=90°,
∴∠AEF=∠B,又∠EAF=∠BAE,
∴△AEF∽△ABE,
∴![]() =
=![]() ,
,
∴AE2=AFAB;
(2)設CE=a,則BE=2a,
∵∠DCB+∠B=90°,∠CAB+∠B=90°,
∴∠DCB=∠CAB,
∵∠GCE=∠GEC,
∴∠CAB=∠GEC,又∠ACE=∠BCA=90°,
∴△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=![]() a,
a,
∴∠CAE=∠BAE=∠AEF=30°,
∴FA=FE,
∵∠GAC=∠GCA=30°,
∴GA=GC,
∵GC=GE,
∴GA=GE,又FA=FE,
∴∠AFG=60°,
∴tan∠AFG=![]() ;
;
(3)設BE=a,CE=EF=b,
∵△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC2=b(a+b),
∴AC=![]() ,
,
∵EF∥AC,
∴△BEF∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得,b2+ab﹣a2=0,
則(![]() )2+
)2+![]() ﹣1=0,
﹣1=0,
解得:![]() =
=![]() ,
,
∴tanB=![]() =
=![]()
故答案為:![]() .
.


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
【題目】某中學為了了解七年級男生入學時的跳繩情況,隨機選取50名剛入學的男生進行個人一分鐘跳繩測試,并以測試數據為樣本,繪制出部分頻數分布表和部分頻數分布直方圖(如圖所示).根據圖表解答下列問題:
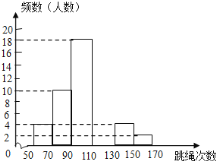
(1)a= ,b= ;
(2)這個樣本數據的中位數落在第 組;
(3)若七年級男生個人一分鐘跳繩次數x≥130時成績為優秀,則從這50名男生中任意選一人,跳繩成績為優秀的概率為多少;
(4)若該校七年級入學時男生共有150人,請估計此時該校七年級男生個人一分鐘跳繩成績為優秀的人數.
組別 | 次數x | 頻數(人數) |
第1組 | 50≤x<70 | 4 |
第2組 | 70≤x<90 | a |
第3組 | 90≤x<110 | 18 |
第4組 | 110≤x<130 | b |
第5組 | 130≤x<150 | 4 |
第6組 | 150≤x<170 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古希臘著名的畢達哥拉斯學派把1,3,6,10…這樣的數稱為“三角形數”,而把1,4,9,16…這樣的數稱為“正方形數”.從圖中可以發現,任何一個大于1的“正方形數”都可以看作兩個相鄰“三角形數”之和.下列等式中,符合這一規律的是( )

A. 36=15+21 B. 25=9+16 C. 13=3+10 D. 49=18+31
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABE中,點A、B是反比例函數y=![]() (k≠0)圖象上的兩點,點E在x軸上,延長線段AB交y軸于點C,點B恰為線段AC中點,過點A作AD⊥x軸于點D.若S△ABE=
(k≠0)圖象上的兩點,點E在x軸上,延長線段AB交y軸于點C,點B恰為線段AC中點,過點A作AD⊥x軸于點D.若S△ABE=![]() ,DE=2OE,則k的值為( )
,DE=2OE,則k的值為( )
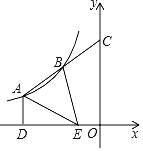
A.6B.﹣6C.9D.﹣9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察算式:![]() ;
;![]() ;
;![]() ;
;![]() ,...請根據你發現的規律填空:
,...請根據你發現的規律填空:
(1)![]() _________.
_________.
(2)用含n 的等式表示上面的規律:__________.
(3)用找到的規律解決下面的問題:計算:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習概率的課堂上,老師提出問題:一口袋裝有除顏色外均相同的2個紅球1個白球和1個籃球,小剛和小明想通過摸球來決定誰去看電影,同學甲設計了如下的方案:第一次隨機從口袋中摸出一球(不放回);第二次再任意摸出一球,兩人勝負規則如下:摸到“一紅一白”,則小剛看電影;摸到“一白一藍”,則小明看電影.
(1)同學甲的方案公平嗎?請用列表或畫樹狀圖的方法說明;
(2)你若認為這個方案不公平,那么請你改變一下規則,設計一個公平的方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,在正方形ABCD中,E是AB上一點,G是AD上一點,∠ECG=45°,那么EG與圖中兩條線段的和相等?證明你的結論.
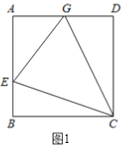
(2)請用(1)中所積累的經驗和知識完成此題,如圖,在四邊形ABCG中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一點,且∠ECG=45°,BE=4,求EG的長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:大數學家高斯在上學讀書時曾經研究過這樣一個問題:1+2+3+…+100=?經過研究,這個問題的一般性結論是1+2+3+…+n=![]() n(n+1),其中n是正整數.現在我們來研究一個類似的問題:1×2+2×3+…n(n+1)=?
n(n+1),其中n是正整數.現在我們來研究一個類似的問題:1×2+2×3+…n(n+1)=?
觀察下面三個特殊的等式:
1×2=![]() (1×2×3﹣0×1×2)
(1×2×3﹣0×1×2)
2×3=![]() (2×3×4﹣1×2×3)
(2×3×4﹣1×2×3)
3×4=![]() (3×4×5﹣2×3×4)
(3×4×5﹣2×3×4)
將這三個等式的兩邊相加,可以得到1×2+2×3+3×4=![]() ×3×4×5=20,
×3×4×5=20,
讀完這段材料,請你思考后回答:
(1)1×2+2×3+…+10×11=________________;
(2)1×2+2×3+3×4+…+n×(n+1)=_________________________;
(3)1×2×3+2×3×4+…+n(n+1)(n+2)=______________________________.
(只需寫出結果,不必寫中間的過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了豐富同學們的課外活動,決定給全校20個班每班配4副乒乓球拍和若干乒乓球,兩家體育用品商店對同一款乒乓球拍和乒乓球推出讓利活動,甲商店買一副乒乓球拍送10個乒乓球,乙商店所有商品均打九折(按標價的90%)銷售,已知2副乒乓球拍和10個乒乓球110元,3副乒乓球拍和20個乒乓球170元。
請解答下列問題:
(1)求每副乒乓球拍和每個乒乓球的單價為多少元.
(2)若每班配4副乒乓球拍和40個乒乓球,則甲商店的費用為 元,乙商店的費用為 元.
(3)每班配4副乒乓球拍和m(m>100)個乒乓球則甲商店的費用為 元,乙商店的費用為 元.
(4)若該校只在一家商店購買,你認為在哪家超市購買更劃算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com