
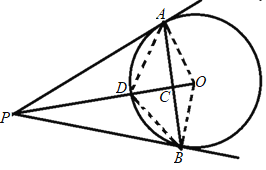
【題目】如圖, 已知點(diǎn)P為⊙O 外一點(diǎn),PA、PB是⊙O的切線(xiàn),切點(diǎn)分別是A、B,連接OP交AB于點(diǎn)C,交⊙O于點(diǎn)D,若PA=3cm, ∠APB=60°,則下列結(jié)論正確的有( )
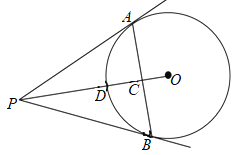
①AB⊥OP;②AC2=PC·OC;③若連接AD,BD,則∠ADB=120°;④PA,PB與劣弧AB圍成的圖形的面積是![]()
A.1個(gè)B.2個(gè)C.3個(gè)D.4個(gè)
【答案】D
【解析】
由切線(xiàn)長(zhǎng)定理結(jié)合圓的半徑相等,可得![]() 是
是![]() 的中垂線(xiàn),可得結(jié)論①,
的中垂線(xiàn),可得結(jié)論①,
證明![]() 可判斷結(jié)論②,
可判斷結(jié)論②,
證明![]() 均為等邊三角形,可判斷結(jié)論③,
均為等邊三角形,可判斷結(jié)論③,
利用PA,PB與劣弧AB圍成的圖形的面積等于四邊形![]() 的面積減去扇形
的面積減去扇形![]() 的面積判斷④.
的面積判斷④.
解:連接OA,OB,則![]()
![]() PA、PB是⊙O的切線(xiàn),
PA、PB是⊙O的切線(xiàn),
![]()
![]() 是
是![]() 的中垂線(xiàn),
的中垂線(xiàn),
![]() 故①正確,
故①正確,
![]() PA是⊙O的切線(xiàn),
PA是⊙O的切線(xiàn),
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 故②正確,
故②正確,
連接AD,BD,
![]()
![]()
![]()
![]()
![]()
![]() 是等邊三角形,
是等邊三角形,
![]()
同理:![]()
![]() 故③正確,
故③正確,
![]()
![]()
![]() S四邊形APBO
S四邊形APBO![]()
![]() 均為等邊三角形,
均為等邊三角形,
![]()
![]() S扇形AOBD
S扇形AOBD![]()
![]() PA,PB與劣弧AB圍成的圖形的面積是
PA,PB與劣弧AB圍成的圖形的面積是![]() .故④正確.
.故④正確.
綜上:①②③④均正確,
故選D.


 課程達(dá)標(biāo)測(cè)試卷闖關(guān)100分系列答案
課程達(dá)標(biāo)測(cè)試卷闖關(guān)100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關(guān)100分系列答案
全能闖關(guān)100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,其對(duì)稱(chēng)軸為直線(xiàn)x=﹣1,與x軸的交點(diǎn)為(x1,0)、(x2,0),其中0<x2<1,有下列結(jié)論:①b2﹣4ac>0;②4a﹣2b+c>﹣1;③﹣3<x1<﹣2;④當(dāng)m為任意實(shí)數(shù)時(shí),a﹣b≤am2+bm;⑤3a+c=0.其中,正確的結(jié)論有( )
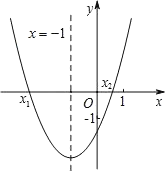
A.②③④B.①③⑤C.②④⑤D.①③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知直線(xiàn)![]() 與雙曲線(xiàn)
與雙曲線(xiàn)![]() 交于 A、B 兩點(diǎn),且點(diǎn)A的橫坐標(biāo)
交于 A、B 兩點(diǎn),且點(diǎn)A的橫坐標(biāo)![]() .
.
(1)求 k 的值;
(2)若雙曲線(xiàn) ![]() 上點(diǎn) C 的縱坐標(biāo)為 3,求△AOC 的面積;
上點(diǎn) C 的縱坐標(biāo)為 3,求△AOC 的面積;
(3)在 y 軸上有一點(diǎn) M,在直線(xiàn) AB 上有一點(diǎn) P,在雙曲線(xiàn)![]() 上有一點(diǎn) N,若四邊形OPNM 是有一組對(duì)角為 60°的菱形,請(qǐng)寫(xiě)出所有滿(mǎn)足條件的點(diǎn) P 的坐標(biāo).
上有一點(diǎn) N,若四邊形OPNM 是有一組對(duì)角為 60°的菱形,請(qǐng)寫(xiě)出所有滿(mǎn)足條件的點(diǎn) P 的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
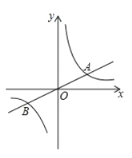
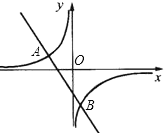
【題目】如圖,一次函數(shù)y=kx+b的圖象與反比例函數(shù)y=![]() 的圖象交于A(﹣2,1),B(1,n)兩點(diǎn).
的圖象交于A(﹣2,1),B(1,n)兩點(diǎn).
(1)求反比例函數(shù)和一次函數(shù)的解析式;
(2)根據(jù)圖象寫(xiě)出使一次函數(shù)的值>反比例函數(shù)的值的x的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】青海新聞網(wǎng)訊:2016年2月21日,西寧市首條綠道免費(fèi)公共自行車(chē)租賃系統(tǒng)正式啟用.市政府今年投資了112萬(wàn)元,建成40個(gè)公共自行車(chē)站點(diǎn)、配置720輛公共自行車(chē).今后將逐年增加投資,用于建設(shè)新站點(diǎn)、配置公共自行車(chē).預(yù)計(jì)2018年將投資340.5萬(wàn)元,新建120個(gè)公共自行車(chē)站點(diǎn)、配置2205輛公共自行車(chē).
(1)請(qǐng)問(wèn)每個(gè)站點(diǎn)的造價(jià)和公共自行車(chē)的單價(jià)分別是多少萬(wàn)元?
(2)請(qǐng)你求出2016年到2018年市政府配置公共自行車(chē)數(shù)量的年平均增長(zhǎng)率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】(2011山東濟(jì)南,27,9分)如圖,矩形OABC中,點(diǎn)O為原點(diǎn),點(diǎn)A的坐標(biāo)為(0,8),點(diǎn)C的坐標(biāo)為(6,0).拋物線(xiàn)![]() 經(jīng)過(guò)A、C兩點(diǎn),與AB邊交于點(diǎn)D.
經(jīng)過(guò)A、C兩點(diǎn),與AB邊交于點(diǎn)D.
(1)求拋物線(xiàn)的函數(shù)表達(dá)式;
(2)點(diǎn)P為線(xiàn)段BC上一個(gè)動(dòng)點(diǎn)(不與點(diǎn)C重合),點(diǎn)Q為線(xiàn)段AC上一個(gè)動(dòng)點(diǎn),AQ=CP,連接PQ,設(shè)CP=m,△CPQ的面積為S.
①求S關(guān)于m的函數(shù)表達(dá)式,并求出m為何值時(shí),S取得最大值;
②當(dāng)S最大時(shí),在拋物線(xiàn)![]() 的對(duì)稱(chēng)軸l上若存在點(diǎn)F,使△FDQ為直角三角形,請(qǐng)直接寫(xiě)出所有符合條件的F的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的對(duì)稱(chēng)軸l上若存在點(diǎn)F,使△FDQ為直角三角形,請(qǐng)直接寫(xiě)出所有符合條件的F的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.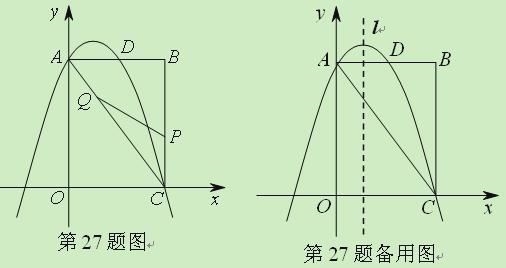
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
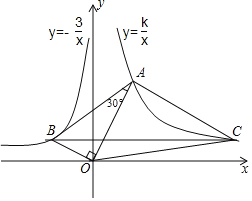
【題目】如圖,已知∠AOB=90°,∠OAB=30°,反比例函數(shù)![]() 的圖象過(guò)點(diǎn)
的圖象過(guò)點(diǎn)![]() ,反比例函數(shù)
,反比例函數(shù)![]() 的圖象過(guò)點(diǎn)A
的圖象過(guò)點(diǎn)A
(1)求![]() 和
和![]() 的值.
的值.
(2)過(guò)點(diǎn)B作BC∥x軸,與雙曲線(xiàn)![]() 交于點(diǎn)C,求△OAC的面積.
交于點(diǎn)C,求△OAC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
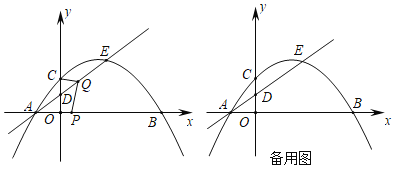
【題目】如圖,在平面直角坐標(biāo)系中,拋物線(xiàn)y=ax2+x+c與直線(xiàn)![]() 交于點(diǎn)A和點(diǎn)E,點(diǎn)A在x軸上.拋物線(xiàn)y=ax2+x+c與x軸另一個(gè)交點(diǎn)為點(diǎn)B,與y軸交于點(diǎn)C(0,
交于點(diǎn)A和點(diǎn)E,點(diǎn)A在x軸上.拋物線(xiàn)y=ax2+x+c與x軸另一個(gè)交點(diǎn)為點(diǎn)B,與y軸交于點(diǎn)C(0,![]() ),直線(xiàn)
),直線(xiàn)![]() 與y軸交于點(diǎn)D.
與y軸交于點(diǎn)D.
(1)求點(diǎn)D的坐標(biāo)和拋物線(xiàn)y=ax2+x+c的函數(shù)表達(dá)式;
(2)動(dòng)點(diǎn)P從點(diǎn)B出發(fā),沿x軸以每秒2個(gè)單位長(zhǎng)度的速度向點(diǎn)A運(yùn)動(dòng),動(dòng)點(diǎn)Q從點(diǎn)A出發(fā)沿射線(xiàn)AE以每秒1個(gè)單位長(zhǎng)度的速度向點(diǎn)E運(yùn)動(dòng),當(dāng)點(diǎn)P到達(dá)點(diǎn)A時(shí),點(diǎn)P、Q同時(shí)停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為t秒,連接AC、CQ、PQ.
①當(dāng)△APQ是以AP為底邊的等腰三角形時(shí),求t的值;
②在點(diǎn)P、Q運(yùn)動(dòng)過(guò)程中,△ACQ的面積記為S1,△APQ的面積記為S2,S=S1+S2,當(dāng)S=![]() 時(shí),請(qǐng)直接寫(xiě)出t的值.
時(shí),請(qǐng)直接寫(xiě)出t的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
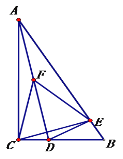
【題目】如圖,△ABC中,已知∠C=90°,∠B=60°,點(diǎn)D在邊BC上,過(guò)D作DE⊥AB于E.
(1)連接AD,取AD的中點(diǎn)F,連接CF,EF,判斷△CEF的形狀,并說(shuō)明理由
(2)若BD=![]() CD.把△BED繞著點(diǎn)D逆時(shí)針旋轉(zhuǎn)m(0<m<180)度后,如果點(diǎn)B恰好落在初始Rt△ABC的邊上,那么m=
CD.把△BED繞著點(diǎn)D逆時(shí)針旋轉(zhuǎn)m(0<m<180)度后,如果點(diǎn)B恰好落在初始Rt△ABC的邊上,那么m=
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com