
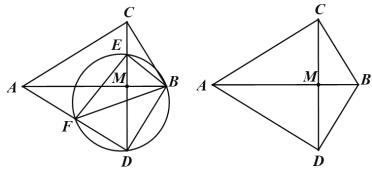
【題目】如圖,在△ABC中,∠ACB=90°,將△ABC沿直線AB翻折得到△ABD,連接CD交AB于點M.E是線段CM上的點,連接BE.F是△BDE的外接圓與AD的另一個交點,連接EF,BF,
(1)求證:△BEF是直角三角形;
(2)求證:△BEF∽△BCA;
(3)當AB=6,BC=m時,在線段CM正存在點E,使得EF和AB互相平分,求m的值.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)想辦法證明∠BEF=90°即可解決問題(也可以利用圓內接四邊形的性質直接證明).
(2)根據兩角對應相等兩三角形相似證明.
(3)證明四邊形AFBE是平行四邊形,推出FJ=![]() BD=
BD=![]() m,EF=m,由△ABC∽△CBM,可得BM=
m,EF=m,由△ABC∽△CBM,可得BM=![]() ,由△BEF∽△BCA,推出
,由△BEF∽△BCA,推出![]() ,由此構建方程求解即可.
,由此構建方程求解即可.
(1)證明:由折疊可知,∠ADB=∠ACB=90°
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2) 證明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3) 設EF交AB于J.連接AE,如下圖所示:
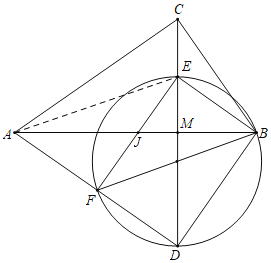
∵EF與AB互相平分,
∴四邊形AFBE是平行四邊形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴ FJ=![]()
∴ EF=![]()
∵ △ABC∽△CBM
∴ BC:MB=AB:BC
∴ BM=![]() ,
,
∵ △BEJ∽△BME,
∴ BE:BM=BJ:BE
∴ BE=![]() ,
,
∵ △BEF∽△BCA,
∴![]()
即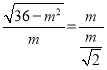
解得![]() (負根舍去).
(負根舍去).
故答案為:![]()


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知:AB是⊙O的直徑,點C在⊙O上,CD是⊙O的切線,AD⊥CD于點D.E是AB延長線上一點,CE交⊙O于點F,連結OC,AC.

(1)求證:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度數.②若⊙O的半徑為![]() ,求線段EF的長.
,求線段EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】黔東南州某超市購進甲、乙兩種商品,已知購進3件甲商品和2件乙商品,需60元;購進2件甲商品和3件乙商品,需65元.
(1)甲、乙兩種商品的進貨單價分別是多少?
(2)設甲商品的銷售單價為x(單位:元/件),在銷售過程中發現:當11≤x≤19時,甲商品的日銷售量y(單位:件)與銷售單價x之間存在一次函數關系,x、y之間的部分數值對應關系如表:
銷售單價x(元/件) | 11 | 19 |
日銷售量y(件) | 18 | 2 |
請寫出當11≤x≤19時,y與x之間的函數關系式.
(3)在(2)的條件下,設甲商品的日銷售利潤為w元,當甲商品的銷售單價x(元/件)定為多少時,日銷售利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形![]() 中,對角線
中,對角線![]() 相交于點
相交于點![]() ,點
,點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() ,將
,將![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() 得到
得到![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .
.
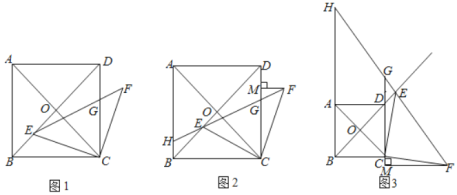
(1)若![]() ,求
,求![]() 的面積;
的面積;
(2)如圖2,線段![]() 的延長線交
的延長線交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,求證:
,求證:![]() ;
;
(3)如圖3,點![]() 為射線
為射線![]() 上一點,線段
上一點,線段![]() 的延長線交直線
的延長線交直線![]() 于點
于點![]() ,交直線
,交直線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 垂直直線
垂直直線![]() 于點
于點![]() ,請直接寫出線段
,請直接寫出線段![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一張寬為1cm的長方形紙片ABCD折疊成如圖所示的陰影圖案,頂點A,D互相重合,中間空白部分是以E為直角頂點,腰長為2cm的等腰直角三角形,則紙片的長AD(單位:cm)為( )
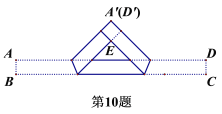
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,AB為
中,AB為![]() 的直徑,C為
的直徑,C為![]() 上一點,P是
上一點,P是![]() 的中點,過點P作AC的垂線,交AC的延長線于點D.
的中點,過點P作AC的垂線,交AC的延長線于點D.
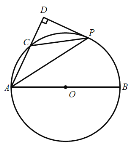
(1)求證:DP是![]() 的切線;
的切線;
(2)若AC=5,![]() ,求AP的長.
,求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在RtΔABC中,∠ABC=90°,AB=CB,以AB為直徑的⊙O交AC于點D,點E是AB邊上一點(點E不與點A、B重合),DE的延長線交⊙O于點G,DF⊥DG,且交BC于點F.
(1)求證:AE=BF;
(2)連接EF,求證:∠FEB=∠GDA;
(3)連接GF,若AE=2,EB=4,求ΔGFD的面積.
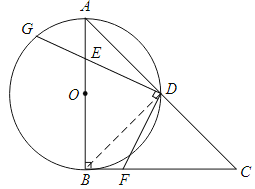
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個矩形紙片![]() ,將該紙片放置在平面直角坐標系中,點
,將該紙片放置在平面直角坐標系中,點![]() ,點
,點![]() ,點P為
,點P為![]() 邊上的動點.
邊上的動點.
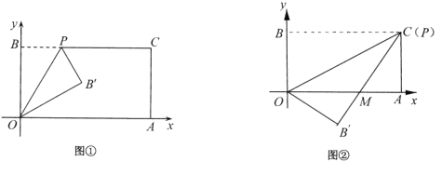
(1)如圖①,經過點O、P折疊該紙片,得點![]() 和折痕
和折痕![]() .當點P的坐標為
.當點P的坐標為![]() 時,求
時,求![]() 的度數;
的度數;
(2)如圖②,當點P與點C重合時,經過點O、P折疊紙片,使點B落在點![]() 的位置,
的位置,![]() 與
與![]() 交于點M,求點M的坐標;
交于點M,求點M的坐標;
(3)過點P作直線![]() ,交
,交![]() 于點Q,再取
于點Q,再取![]() 中點T,
中點T,![]() 中點N,分別以
中點N,分別以![]() ,
,![]() ,
,![]() ,
,![]() 為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段
為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段![]() 上,A、C的對應點也恰好重合,也落在線段
上,A、C的對應點也恰好重合,也落在線段![]() 上,求此時點P的坐標(直接寫出結果即可).
上,求此時點P的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝公司有![]() 型童裝80件,
型童裝80件,![]() 型童裝120件,分配給下屬的“萬達”和“萬象城”兩個專賣店銷售,其中140件給萬達店,60件給萬象城店,且都能賣完,兩商店銷售這兩種童裝每件的利潤(元)如表:
型童裝120件,分配給下屬的“萬達”和“萬象城”兩個專賣店銷售,其中140件給萬達店,60件給萬象城店,且都能賣完,兩商店銷售這兩種童裝每件的利潤(元)如表:
|
| |
萬達店 | 100 | 80 |
萬象城店 | 80 | 90 |
(1)設分配給萬達店![]() 型產品
型產品![]() 件(
件(![]() ),請在下表中用含
),請在下表中用含![]() 的代數式填寫:
的代數式填寫:
|
| |
萬達店 |
| ______ |
萬象城店 | ______ | ______ |
若記這家服裝公司賣出這200件產品的總利潤為![]() (元),求
(元),求![]() 關于
關于![]() 的函數關系.
的函數關系.
(2)現要求總利潤不低于18140元,請說明有多少種不同分配方案,并寫出各種分配方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com