
觀察計算:
當 ,
,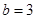 時,
時,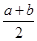 與
與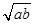 的大小關系是_________________.
的大小關系是_________________.
當 ,
, 時,
時,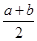 與
與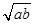 的大小關系是_________________.
的大小關系是_________________.
探究證明:
如圖所示, 為圓O的內接三角形,
為圓O的內接三角形,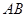 為直徑,過C作
為直徑,過C作 于D,設
于D,設 ,BD=b.
,BD=b.

(1)分別用 表示線段OC,CD;
表示線段OC,CD;
(2)探求OC與CD表達式之間存在的關系(用含a,b的式子表示).
歸納結論:
根據上面的觀察計算、探究證明,你能得出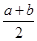 與
與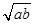 的大小關系是:______________.
的大小關系是:______________.
實踐應用:
要制作面積為4平方米的長方形鏡框,直接利用探究得出的結論,求出鏡框周長的最小值.
觀察計算:當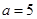 ,
, 時,
時,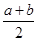 >
> ;當
;當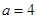 ,
,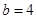 時,
時,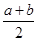 =
= .
.
探究證明:(1)OC=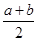 ,
,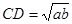 ;
;
(2)當a=b時,OC=CD,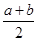 =
= ;a≠b時,OC>CD,
;a≠b時,OC>CD,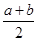 >
> .
.
結論歸納: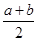

 .
.
實踐應用:周長最小為4米.
【解析】
試題分析:觀察計算:把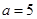 ,
, 和
和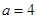 ,
,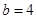 分別代入
分別代入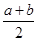 與
與 計算,即可作出判斷;
計算,即可作出判斷;
探究證明:(1)由于OC是直徑AB的一半,則OC易得.通過證明△ACD∽△CBD,可求CD;
(2)分a=b,a≠b討論可得出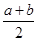 與
與 的大小關系;
的大小關系;
實踐應用:通過前面的結論長方形為正方形時,周長最小.
試題解析:觀察計算:當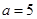 ,
, 時,
時,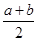 >
>
當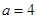 ,
,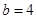 時,
時,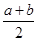 =
= .
.
探究證明:
(1)∵AB=AD+BD=2OC,
∴OC=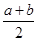
∵AB為⊙O直徑,
∴∠ACB=90°.
∵∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∴△ACD∽△CBD.
∴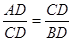 .即CD2=AD•BD=ab,解得
.即CD2=AD•BD=ab,解得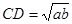 ;
;
(2)當a=b時,OC=CD,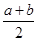 =
= ;
;
a≠b時,OC>CD,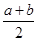 >
> .
.
結論歸納: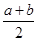

 .
.
實踐應用
設長方形一邊長為x米,則另一邊長為 米,設鏡框周長為l米,
米,設鏡框周長為l米,
則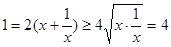 ,當
,當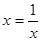 ,即x=1(米)時,鏡框周長最小.
,即x=1(米)時,鏡框周長最小.
此時四邊形為正方形時,周長最小為4米.
考點:1.幾何不等式;2.相似三角形的判定與性質;3.圓周角定理


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
| a2+24 |
| a2+24 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 附加題.觀察計算
附加題.觀察計算| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com