
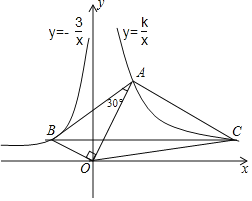
【題目】如圖,已知∠AOB=90°,∠OAB=30°,反比例函數![]() 的圖象過點
的圖象過點![]() ,反比例函數
,反比例函數![]() 的圖象過點A
的圖象過點A
(1)求![]() 和
和![]() 的值.
的值.
(2)過點B作BC∥x軸,與雙曲線![]() 交于點C,求△OAC的面積.
交于點C,求△OAC的面積.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)把點B![]() 代入
代入![]() 可求出a值,進而可求出OE、BE的長,分別過點A、B作AD⊥x軸于D,BE⊥x軸于E,可證明△BOE∽△OAD,根據相似三角形的性質及正切的定義可得
可求出a值,進而可求出OE、BE的長,分別過點A、B作AD⊥x軸于D,BE⊥x軸于E,可證明△BOE∽△OAD,根據相似三角形的性質及正切的定義可得![]() ,即可求出AD和OD的長,可得A點坐標,代入
,即可求出AD和OD的長,可得A點坐標,代入![]() 即可求出k值;(2)過點C作CF⊥x軸于F,由B點坐標可知C點縱坐標,由C點在
即可求出k值;(2)過點C作CF⊥x軸于F,由B點坐標可知C點縱坐標,由C點在![]() 圖象上,可求出C點橫坐標,可得CF的長,由點A、點C在反比例函數
圖象上,可求出C點橫坐標,可得CF的長,由點A、點C在反比例函數![]() 圖象上,可得S△AOD=S△COF,根據
圖象上,可得S△AOD=S△COF,根據![]()
![]() 即可得答案.
即可得答案.
(1)∵反比例函數![]() 經過點B
經過點B![]()
∴![]()
∴OE=3,BE=1,
如圖,分別過點A、B作AD⊥x軸于D,BE⊥x軸于E,
∵∠AOB=90°,
∴∠EOB+∠AOD=90°,
∵∠AOD+∠OAD=90°,
∴∠EOB=∠OAD,
又∵∠BEO=∠ODA=90°,
∴△BOE∽△OAD,
∴![]() ,
,
∴AD=![]() OE=3
OE=3![]() ,OD=
,OD=![]() BE=
BE=![]() ,
,
∴![]() ,
,
∴![]() .
.
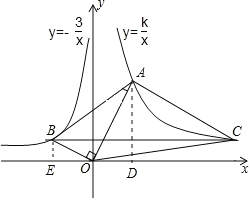
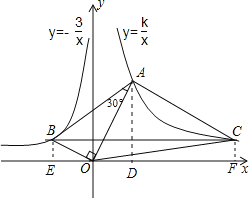
(2)如圖,過點C作CF⊥x軸于F
由(1)可知AD=![]() ,OD=
,OD=![]() ,
,
∵BC∥x軸,B(-3,1),
∴![]() =1,
=1,
∵點C在雙曲線![]() 上,
上,
∴![]() =9,
=9,
∴C(9,1),
∴CF=1,
∵點A、點C在反比例函數![]() 圖象上,
圖象上,
∴S△AOD=S△COF,
∴![]()
![]() ,
,
∴![]()
![]()
![]() .
.


 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知點A1(1,1),將點A1向上平移1個單位長度,再向右平移2個單位長度得到點A2;將點A2向上平移2個單位長度,再向右平移4個單位長度得到點A3;將點A3向上平移4個單位長度,再向右平移8個單位長度得到點A4,…按這個規律平移下去得到點An(n為正整數),則點An的坐標是( )
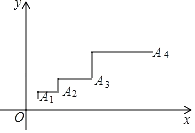
A.(2n,2n﹣1)B.(2n﹣1,2n)
C.(2n﹣1,2n+1)D.(2n﹣1,2n﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設一次函數y1=x+a+b和二次函數y2=x(x+a)+b.
(1)若y1,y2的圖象都經過點(-2,1),求這兩個函數的表達式;
(2)求證:y1,y2的圖象必有交點;
(3)若a>0,y1,y2的圖象交于點(x1,m),(x2,n)(x1<x2),設(x3,n)為y2圖象上一點(x3≠x2),求x3-x1的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①所示,已知正方形ABCD和正方形AEFG,G、A、B在同一直線上,點E在AD上,連接DG,BE.
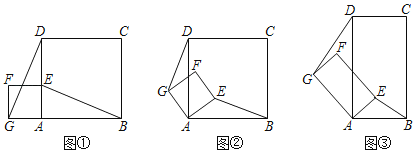
(1)證明:BE=DG;
(2)發現:當正方形AEFG繞點A旋轉,如圖②所示,判斷BE與DG的數量關系和位置關系,并說明理由;
(3)探究:如圖③所示,若四邊形ABCD與四邊形AEFG都為矩形,且AD=2AB,AG=2AE時,判斷BE與DG的數量關系和位置關系是否與(2)的結論相同,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了幫助本市一名患“白血病”的高中生,某班15名同學積極捐款,他們捐款數額如下表:
捐款的數額(單位:元) | 5 | 10 | 20 | 50 | 100 |
人數(單位:個) | 2 | 4 | 5 | 3 | 1 |
關于這15名同學所捐款的數額,下列說法正確的是
A.眾數是100 B.平均數是30 C.極差是20 D.中位數是20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,按以下步驟作圖:①分別以點B和點C為圓心,大于![]() BC的長為半徑作弧,兩弧相交于點M和N;②作直線MN,分別交邊AB,BC于點D和E,連接CD.若∠BCA=90°,AB=8,則CD的長為_____.
BC的長為半徑作弧,兩弧相交于點M和N;②作直線MN,分別交邊AB,BC于點D和E,連接CD.若∠BCA=90°,AB=8,則CD的長為_____.
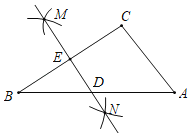
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,某超市從底樓到二樓有一自動扶梯,圖2是側面示意圖.已知自動扶梯AB的長度是12.5米,MN是二樓樓頂,MN∥PQ,C是MN上處在自動扶梯頂端B點正上方的一點,BC⊥MN,在自動扶梯底端A處測得C點的仰角∠CAQ為45°,坡角∠BAQ為37°,求二樓的層高BC(精確到0.1米).(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75 )
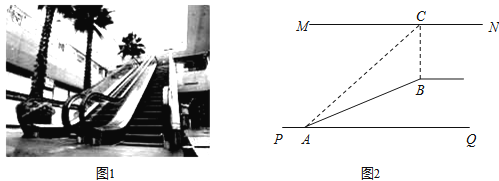
查看答案和解析>>
科目:初中數學 來源: 題型:
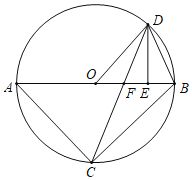
【題目】如圖,已知△ABC內接于⊙O,AB是直徑,點D在⊙O上,OD∥BC,過點D作DE⊥AB,垂足為E,連接CD交OE邊于點F.
(1)求證:△DOE∽△ABC;
(2)求證:∠ODF=∠BDE;
(3)連接OC.設△DOE的面積為S.sinA=![]() ,求四邊形BCOD的面積(用含有S的式子表示)
,求四邊形BCOD的面積(用含有S的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
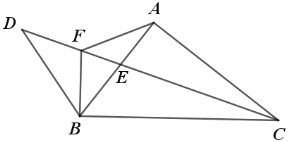
【題目】如圖,Rt△ABC 中,∠BAC=90°,CE 平分∠ACB,點 D 在 CE的延長線上,連接 BD,過B作BF⊥BC交 CD 于點 F,連接 AF,若CF=2BD ,DE:CE=5:8 , BF ![]() ,則AF的長為_________.
,則AF的長為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com