
【題目】如圖1,若四邊形ABCD、GFED都是正方形,顯然圖中有AG=CE,AG⊥CE.
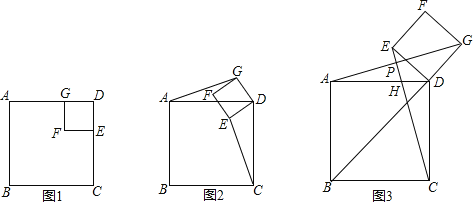
(1)當正方形GFED繞D旋轉到如圖2的位置時,AG=CE是否成立?若成立,請給出證明,若不成立,請說明理由;
(2)當正方形GFED繞D旋轉到B,D,G在一條直線(如圖3)上時,連結CE,設CE分別交AG、AD于P、H.
①求證:AG⊥CE;
②如果,AD=2![]() ,DG=
,DG=![]() ,求CE的長.
,求CE的長.
【答案】(1)AG=CE成立;(2)①詳見解析;②5![]()
【解析】
(1)利用正方形性質以及全等三角形的判定的很粗△AGD≌△CED(SAS)即可得出答案;
(2)①根據(1)得出∠1=∠2,再利用∠3=∠4,∠4+∠2=90°,可得出∠3+∠1=90°,進而得出答案;
②利用等腰直角三角形的性質可得出MD=MG=![]() ,進而利用勾股定理求出CE的長.
,進而利用勾股定理求出CE的長.
(1)解:AG=CE成立.
理由:∵四邊形ABCD、四邊形DEFG是正方形,
∴GD=DE,AD=DC,
∠GDE=∠ADC=90°,
∴∠GDA=90°﹣∠ADE=∠EDC,
在△AGD和△CED中,
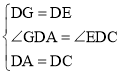
∴△AGD≌△CED(SAS),
∴AG=CE;
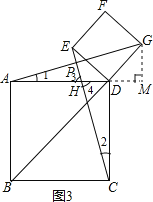
(2)證明:①由(1)可知△AGD≌△CED,
∴∠1=∠2,
∵∠3=∠4,∠4+∠2=90°,
∴∠3+∠1=90°,
∴∠APH=90°,
∴AG⊥CH;
②解:過G作GM⊥AD于M.
∵BD是正方形ABCD的對角線,
∴∠ADB=∠GDM=45°,
∴∠DGM=45°,
∵DG=![]() ,
,
∴MD=MG=![]() ,
,
在Rt△AMG中,由勾股定理,得
∴CE=AG=5![]() .
.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:
【題目】某市居民的交通消費可分為交通工具、交通工具使用燃料、交通工具維修、市內公共交通、城市間交通五項.該市統計局根據當年各項的權重及各項價格的漲幅,計算當年居民交通消費價格的平均漲幅.2017年該市的有關數據如下表所示.
交通工具 | 交通工具使用燃料 | 交通工具維修 | 市內公共交通 | 城市間交通 | |
占交通消費的比例 | 22% | 13% | 5% | P | 26% |
相對上一年價格的漲幅 | 1.5% | m% | 2% | 0.5% | 1% |
(1)求p的值;
(2)若2017年該市的居民交通消費相對上一年價格的平均漲幅為1.25%,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2-2(k-1)x+k2 =0有兩個實數根x1.x2.
(1)求實 數k的取值范圍;
(2)若(x1+1)(x2+1)=2,試求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面坐標系xOy中,點A的坐標為(1,0),點P的橫坐標為2,將點A繞點P旋轉,使它的對應點B恰好落在x軸上(不與A點重合);再將點B繞點O逆時針旋轉90°得到點C.
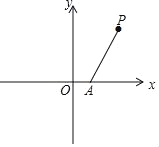
(1)直接寫出點B和點C的坐標;
(2)求經過A,B,C三點的拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
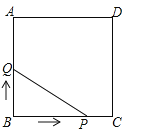
【題目】(3分)如圖,正方形ABCD的邊長為3cm,動點P從B點出發以3cm/s的速度沿著邊BC﹣CD﹣DA運動,到達A點停止運動;另一動點Q同時從B點出發,以1cm/s的速度沿著邊BA向A點運動,到達A點停止運動.設P點運動時間為x(s),△BPQ的面積為y(cm2),則y關于x的函數圖象是( )
A.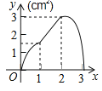 B.
B.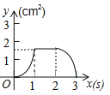 C.
C.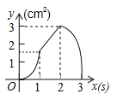 D.
D.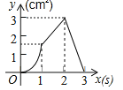
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一張矩形紙片![]() 中,
中,![]() ,
,![]() ,現將這張紙片按下列圖示方法折疊,請解決下列問題:
,現將這張紙片按下列圖示方法折疊,請解決下列問題:
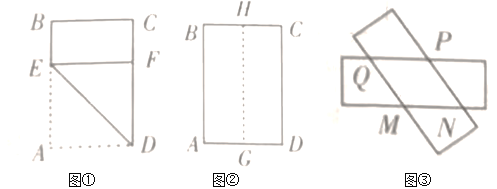
(1)如圖①,折痕為![]() ,點
,點![]() 的對應點
的對應點![]() 在
在![]() 上,求證:四邊形
上,求證:四邊形![]() 是正方形;
是正方形;
(2)如圖②,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,把矩形紙片
的中點,把矩形紙片![]() 沿著
沿著![]() 剪開,變成兩張矩形紙片,將兩張紙片任意疊合后(如圖③),判斷重疊四邊形
剪開,變成兩張矩形紙片,將兩張紙片任意疊合后(如圖③),判斷重疊四邊形![]() 的形狀,并證明;
的形狀,并證明;
(3)在(2)中,重疊四邊形![]() 的周長是否存在最大值或最小值?若存在,請求出最大值或最小值;若不存在,請說明理由.
的周長是否存在最大值或最小值?若存在,請求出最大值或最小值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:二次函數y=x2﹣mx+![]() m+1(m為常數).若這個二次函數的圖象與x軸只有一個公共點A,且A點在x軸的正半軸上.
m+1(m為常數).若這個二次函數的圖象與x軸只有一個公共點A,且A點在x軸的正半軸上.
(1)求m的值.
(2)四邊形AOBC是正方形,且點B在y軸的負半軸上,現將這個二次函數的圖象平移,使平移后的函數圖象恰好經過B,C兩點,求平移后的圖象對應的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
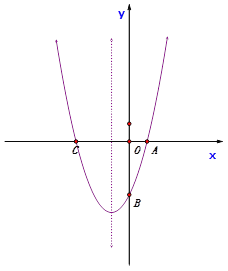
【題目】如圖,已知拋物線![]() 經過點A(1,0)和點B (0,-3),與x軸交于另一點C。
經過點A(1,0)和點B (0,-3),與x軸交于另一點C。
(1)求拋物線的解析式。
(2)在拋物線上是否存在一點D,使△ACD的面積與△ABC的面積相等(點D不與點B重合)?若存在,求出點D的坐標;若不存在,請說明理由。
(3)若點P是拋物線上的動點,點Q是拋物線對稱軸上的動點,那么是否存在這樣的點P,使以點A、C、P、Q為頂點的四邊形為平行四邊形?若存在,求出點P的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形 ABCD 的邊長為 8,E 是 BC 邊的中點,點 P 在射線 AD 上, 過 P 作 PF⊥AE 于 F.
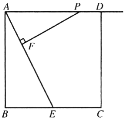
(1)請判斷△PFA 與△ABE 是否相似,并說明理由;
(2)當點 P 在射線 AD 上運動時,設 PA=x,是否存在實數 x,使以 P,F,E 為頂 點的三角形也與△ABE 相似?若存在,請求出 x 的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com