
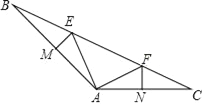
【題目】如圖,已知△ABC中∠BAC=135°,點E,點F在BC上,EM垂直平分AB交AB于點M,FN垂直平分AC交AC于點N,BE=12,CF=9.
(1)判斷△EAF的形狀,并說明理由;
(2)求△EAF的周長.
【答案】(1)△EAF為直角三角形.理由見解析;(2)△EAF的周長=36.
【解析】
(1)根據線段垂直平分線的性質得出BE=AE,AF=CF,再由∠BAC=135°得出∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,故∠BAE+∠CAF=45°,∠EAF=135°﹣45°=90°由此可得出結論;
(2)由(1)知△EAF是直角三角形,再根據勾股定理求出EF的長,進而可得出結論.
(1)△EAF為直角三角形.
∵EM是AB的垂直平分線,
∴BE=AE,
∴∠BAE=∠B.
∵FN是AC的垂直平分線,
∴AF=CF,
∴∠CAF=∠C
.∵∠BAC=135°,
∴∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,
∴∠BAE+∠CAF=45°,
∴∠EAF=135°﹣45°=90°,
∴△EAF為直角三角形;
(2)在△EAF中,
∵∠EAF=90°,
∴EF2=AE2+AF2,
∵BE=12,CF=9,
∴EF2=122+92=225,
∴EF=15,
∴△EAF的周長=12+9+15=36.
故答案為:(1)△EAF為直角三角形.理由見解析;(2)△EAF的周長=36.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】一幢房屋的側面外墻壁的形狀如圖所示,它由等腰三角形OCD和矩形ABCD組成,∠OCD=25°,外墻壁上用涂料涂成顏色相同的條紋,其中一塊的形狀是四邊形EFGH,測得FG∥EH,GH=2.6m,∠FGB=65°.
(1)求證:GF⊥OC;
(2)求EF的長(結果精確到0.1m).
(參考數據:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于給定的兩個函數,任取自變量x的一個值,當x<0時,它們對應的函數值互為相反數;當x≥0時,它們對應的函數值相等,我們稱這樣的兩個函數互為相關函數.例如:一次函數y=x﹣1,它的相關函數為y= ![]() .
.
(1)已知點A(﹣5,8)在一次函數y=ax﹣3的相關函數的圖象上,求a的值;
(2)已知二次函數y=﹣x2+4x﹣ ![]() .①當點B(m,
.①當點B(m, ![]() )在這個函數的相關函數的圖象上時,求m的值;
)在這個函數的相關函數的圖象上時,求m的值;
②當﹣3≤x≤3時,求函數y=﹣x2+4x﹣ ![]() 的相關函數的最大值和最小值;
的相關函數的最大值和最小值;
(3)在平面直角坐標系中,點M,N的坐標分別為(﹣ ![]() ,1),(
,1),( ![]() ,1),連結MN.直接寫出線段MN與二
,1),連結MN.直接寫出線段MN與二
次函數y=﹣x2+4x+n的相關函數的圖象有兩個公共點時n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1∥l2,以直線l1上的點A為圓心,適當長為半徑畫弧,分別交直線l1和l2于B、C兩點,連接AC、BC,若∠ABC=65°,則∠1的度數是( )

A. 35° B. 50° C. 65° D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△PQR在直角坐標系中的位置如圖所示:
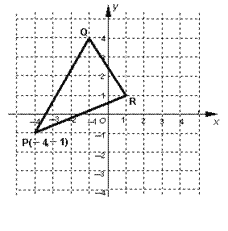
(1) 求出△PQR的面積;
(2) 畫出△P′Q′R′,使△P′Q′R′與△PQR關于y軸對稱,寫出點P′、Q′、R′的坐標;
(3)連接PP′,QQ′,判斷四邊形QQ′P′P的形狀,求出四邊形QQ′P′P的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分線.以O為圓心,OC為半徑作⊙O.
(1)求證:AB是⊙O的切線.
(2)已知AO交⊙O于點E,延長AO交⊙O于點D,tanD= ![]() ,求
,求 ![]() 的值.
的值.
(3)在(2)的條件下,設⊙O的半徑為3,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A,B分別是x軸、y軸上的動點,點C,D是某個函數圖象上的點,當四邊形ABCD(A,B,C,D各點依次排列)為正方形時,我們稱這個正方形為此函數圖象的“伴侶正方形”.
例如:在圖1中,正方形ABCD是一次函數y=x+1圖象的其中一個“伴侶正方形”.
(1)如圖1,若某函數是一次函數y=x+1,求它的圖象的所有“伴侶正方形”的邊長;
(2)如圖2,若某函數是反比例函數 ![]() (k>0),它的圖象的“伴侶正方形”為ABCD,點D(2,m)(m<2)在反比例函數圖象上,求m的值及反比例函數的解析式;
(k>0),它的圖象的“伴侶正方形”為ABCD,點D(2,m)(m<2)在反比例函數圖象上,求m的值及反比例函數的解析式;
(3)如圖3,若某函數是二次函數y=ax2+c(a≠0),它的圖象的“伴侶正方形”為ABCD,C,D中的一個點坐標為(3,4),請你直接寫出該二次函數的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com