
【題目】如圖,已知△ABC三個頂點的坐標分別是A(-2,3),B(-3,-1),C(-1,1)
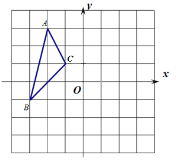
(1)畫出△ABC繞點O逆時針旋轉90°后的△A1B1C1,并寫出點A1的坐標;
(2)畫出△ABC繞點O逆時針旋轉180°后的△A2B2C2,并寫出點A2的坐標;
(3)直接回答:∠AOB與∠A2OB2有什么關系?
【答案】(1)作圖見解析,(-4,-2);(2)作圖見解析,(2,-3);(3)相等.
【解析】
試題分析:(1)根據旋轉的性質作圖,寫出點的坐標;
根據旋轉的性質作圖,寫出點的坐標;
(3)根據旋轉的性質得出結論.
試題解析:(1)作圖如下,點A1的坐標(-4,-2).
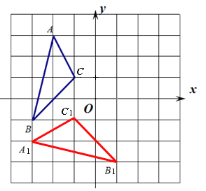
(2)作圖如下,點A2的坐標(2,-3).
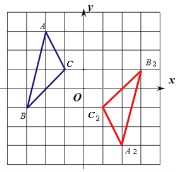
(3)相等.
考點:1.旋轉作圖;2.旋轉的性質.
【題型】解答題
【結束】
20
【題目】已知函數y=(m﹣2)xm2+m-4 +2x﹣1是一個二次函數,求該二次函數的解析式.
 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:初中數學 來源: 題型:
【題目】“閱讀素養的培養是構建核心素養的重要基礎,重慶十一中學校以‘大閱讀’特色課程實施為突破口,著力提升學生的核心素養.”全校師生積極響應和配合,開展各種活動豐富其課余生活.在數學興趣小組中,同學們從書上認識了很多有趣的數.其中有一個“和平數”引起了同學們的興趣.描述如下:一個四位數,記千位上和百位上的數字之和為x,十位上和個位上的數字之和為y,如果![]() ,那么稱這個四位數為“和平數”.
,那么稱這個四位數為“和平數”.
例如:1423,![]() ,
,![]() ,因為
,因為![]() ,所以1423是“和平數”.
,所以1423是“和平數”.
(1)直接寫出:最小的“和平數”是________,最大的“和平數”是__________;
(2)求同時滿足下列條件的所有“和平數”:
①個位上的數字是千位上的數字的兩倍;
②百位上的數字與十位上的數字之和是12的倍數;
(3)將一個“和平數”的個位上與十位上的數字交換位置,同時,將百位上與千位上的數字交換位置,稱交換前后這兩個“和平數”為“相關和平數”.
例如:1423于4132為“相關和平數”
求證:任意的兩個“相關和平數”之和是1111的倍數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知點A、B是反比例函數y=﹣![]() 上在第二象限內的分支上的兩個點,點C(0,3),且△ABC滿足AC=BC,∠ACB=90°,則線段AB的長為__.
上在第二象限內的分支上的兩個點,點C(0,3),且△ABC滿足AC=BC,∠ACB=90°,則線段AB的長為__.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是射線
是射線![]() 上一動點,以
上一動點,以![]() 為邊向右側作等邊
為邊向右側作等邊![]() ,點
,點![]() 的位置隨著點
的位置隨著點![]() 的位置變化而變化.
的位置變化而變化.

(1)如圖1,當點![]() 在四邊形
在四邊形![]() 內部或邊上時,連接
內部或邊上時,連接![]() ,
,![]() 與
與![]() 的數量關系是________,
的數量關系是________,![]() 與
與![]() 的位置關系是_______;
的位置關系是_______;
(2)如圖2,當點![]() 在四邊形
在四邊形![]() 外部時,(1)中的結論是否還成立?若成立,請予以證明;
外部時,(1)中的結論是否還成立?若成立,請予以證明;
(3)如圖3,當點![]() 在線段
在線段![]() 的延長線上時,連接
的延長線上時,連接![]() ,若
,若![]() ,
,![]() ,則線段
,則線段![]() ______,
______,![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填在相應的大括號內:25,-0.91,![]() ,3.14,-7,0,-50,
,3.14,-7,0,-50,![]() ,9.
,9.
(1)整數有:{ }; (2)分數有:{ };
(3)正整數有:{ }; (4)負整數有:{ };
(5)正分數有:{ }; (6)負分數有:{ };
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,點D在邊BC所在的直線上,過點D作DF∥AC交直線AB于點F,DE∥AB交直線AC于點E.
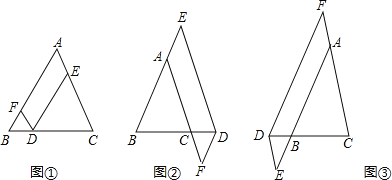
(1)當點D在邊BC上時,如圖①,求證:DE+DF=AC.
(2)當點D在邊BC的延長線上時,如圖②;當點D在邊BC的反向延長線上時,如圖③,請分別寫出圖②、圖③中DE,DF,AC之間的數量關系,不需要證明.
(3)若AC=6,DE=4,則DF= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com