
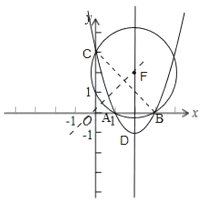
【題目】已知拋物線![]() .
.
(1)該拋物線的對稱軸是![]() ________.
________.
(2)該拋物線與![]() 軸交于點
軸交于點![]() ,點
,點![]() 與
與![]() 軸交于點
軸交于點![]() ,點
,點![]() 的坐標為
的坐標為![]() ,若此拋物線的對稱軸上的點
,若此拋物線的對稱軸上的點![]() 滿足
滿足![]() ,則點
,則點![]() 的縱坐標
的縱坐標![]() 的取值范圍是________.
的取值范圍是________.
【答案】2 ![]() 或
或![]()
【解析】
(1)根據拋物線的對稱軸為![]() 進行求解;
進行求解;
(2)根據二次函數的性質可求出點B,C的坐標,作BC的垂線交對稱軸于點F,以點F為圓心,以FB為半徑作⊙F,得到△ABC的外接圓,根據兩點間距離公式可求出圓心F的坐標以及外接圓半徑,然后根據圓的性質可得點P在第一象限時,點![]() 的縱坐標
的縱坐標![]() 的取值范圍,同理可得點P在第四象限時,點
的取值范圍,同理可得點P在第四象限時,點![]() 的縱坐標
的縱坐標![]() 的取值范圍.
的取值范圍.
解:(1)該拋物線的對稱軸是![]() ,
,
故答案為:2;
(2)∵點![]() 的坐標為
的坐標為![]() ,拋物線的對稱軸是
,拋物線的對稱軸是![]() ,
,
∴點B的坐標為(3,0),
將點![]() 代入
代入![]() 可得:a=1,
可得:a=1,
∴4a-1=3,即點C的坐標為(0,3),
如圖,作BC的垂線交對稱軸于點F,以點F為圓心,以FB為半徑作⊙F,得到△ABC的外接圓,設點F坐標為(2,m),
由FA=FC可得:![]() ,
,
解得:m=2,
∴點F的坐標為(2,2),FA=![]() ,
,
∴當∠APB<∠ACB,且點P在第一象限時,點![]() 的縱坐標
的縱坐標![]() 的取值范圍是:
的取值范圍是:![]() ,
,
同理可得,點P在第四象限時,點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() .
.
綜上所述,點的縱坐標![]() 的取值范圍是:
的取值范圍是:![]() 或
或![]() ,
,
故答案為:![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】設二次函數![]() 的圖象為C1.二次函數
的圖象為C1.二次函數![]() 的圖象與C1關于y軸對稱.
的圖象與C1關于y軸對稱.

(1)求二次函數![]() 的解析式;
的解析式;
(2)當![]() ≤0時,直接寫出
≤0時,直接寫出![]() 的取值范圍;
的取值范圍;
(3)設二次函數![]() 圖象的頂點為點A,與y軸的交點為點B,一次函數
圖象的頂點為點A,與y軸的交點為點B,一次函數![]() ( k,m為常數,k≠0)的圖象經過A,B兩點,當
( k,m為常數,k≠0)的圖象經過A,B兩點,當![]() 時,直接寫出x的取值范圍.
時,直接寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
小明遇到下面一個問題:
如圖1所示,![]() 是
是![]() 的角平分線,
的角平分線,![]() ,求
,求![]() 的值.
的值.
小明發現,分別過![]() ,
,![]() 作直線
作直線![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() .通過推理計算,可以解決問題(如圖2).請回答,
.通過推理計算,可以解決問題(如圖2).請回答,![]() ________.
________.

參考小明思考問題的方法,解決問題:
如圖3,四邊形![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,
,![]() .
.![]() 與
與![]() 相交于點
相交于點![]() .
.

(1)![]() =______.
=______.
(2)![]() =__________.
=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
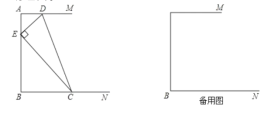
【題目】如圖,已知![]() ,
,![]() ,
,![]() ,點
,點![]() 是射線
是射線![]() 上的一個動點(點
上的一個動點(點![]() 與點
與點![]() 不重合),點
不重合),點![]() 是線段
是線段![]() 上的一個動點(點
上的一個動點(點![]() 與點
與點![]() 不重合),連接
不重合),連接![]() ,過點
,過點![]() 作
作![]() 的垂線,交射線
的垂線,交射線![]() 于點
于點![]() 連接
連接![]() .設
.設![]()
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的函數關系式,并寫出它的定義域;
的函數關系式,并寫出它的定義域;
(2)在(1)的條件下,取線段![]() 的中點
的中點![]() ,連接
,連接![]() ,若
,若![]() ,求
,求![]() 的長;
的長;
(3)如果動點![]() 在運動時,始終滿足條件
在運動時,始終滿足條件![]() 那么請探究:
那么請探究:![]() 的周長是否隨著動點
的周長是否隨著動點![]() 的運動而發生變化?請說明理由。
的運動而發生變化?請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,⊙M的半徑為2,圓心M的坐標為(3,4),點P是⊙M上的任意一點,PA⊥PB,且PA、PB與x軸分別交于A、B兩點,若點A、點B關于原點O對稱,則AB的最小值為( )
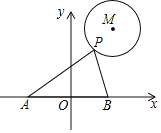
A. 3B. 4C. 6D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
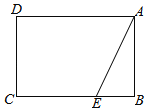
【題目】已知矩形ABCD中,AB=2,BC=m,點E是邊BC上一點,BE=1,連接AE.
(1)沿AE翻折△ABE使點B落在點F處,
①連接CF,若CF∥AE,求m的值;
②連接DF,若![]() ≤DF≤
≤DF≤![]() ,求m的取值范圍.
,求m的取值范圍.
(2)△ABE繞點A順時針旋轉得△AB1E1,點E1落在邊AD上時旋轉停止.若點B1落在矩形對角線AC上,且點B1到AD的距離小于![]() 時,求m的取值范圍.
時,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若點A(3,4)是反比例函數![]() 圖象上一點,則下列說法正確的是( )
圖象上一點,則下列說法正確的是( )
A. 圖象分別位于二、四象限B. 點(2,﹣6)在函數圖象上
C. 當x<0時,y隨x的增大而減小D. 當y≤4時,x≥3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一張長12dm,寬6dm的長方形紙板,將紙板四個角各剪去一個同樣的邊長為xdm的正方形,然后將四周突出部分折起,可制成一個無蓋長方體紙盒.
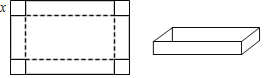
(1)無蓋方盒盒底的長為 dm,寬為 dm(用含x的式子表示).
(2)若要制作一個底面積是40dm2的一個無蓋長方體紙盒,求剪去的正方形邊長x.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com