
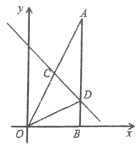
【題目】如圖,在△AOB中,∠ABO=90°,OB=4,AB=8,直線y=-x+b分別交OA、AB于點C、D,且ΔBOD的面積是4.
(1)求直線AO的解析式;
(2)求直線CD的解析式;
(3)若點M是x軸上的點,且使得點M到點A和點C的距離之和最小,求點的坐標.
【答案】(1)y=2x; (2)![]() ;(3)點M的坐標為(
;(3)點M的坐標為(![]() ,0).
,0).
【解析】
(1)先求出點A的坐標,然后設直線AO的解析式為y=kx,用待定系數法求解即可;
(2)由面積法求出BD的長,從而求出點D的坐標,然后帶入y=-x+b求解即可;
(3)先求出點C的坐標,作點C關于x軸的對稱點E,此時M到A、C的距離之和最小,求出直線AE的解析式,即可求出點M的坐標.
(1)![]() OB=4,AB=8,∠ABO=90°,
OB=4,AB=8,∠ABO=90°,
∴A點坐標為(4,8),
設直線AO的解析式為y=kx,則4k=8 ,
解得k=2,即直線AO的解析式為y=2x;
(2)![]() OB=4,∠ABO=90°,
OB=4,∠ABO=90°,![]() =4,
=4,
∴DB=2,∴D點的坐標為(4,2),
把D(4,2)代入![]() 得:
得:![]() =6,
=6,
∴直線CD的解析式為![]() ;
;
(3)由直線![]() 與直線
與直線![]() 組成方程組為
組成方程組為![]() ,
,
解得:![]() ,
,
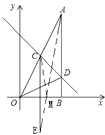
∴點C的坐標為(2,4)
如圖,設點M使得MC+MA最小,作點C關于x軸的對稱點E,可得點E的坐標為(2,-4),連結MC、ME、AE,可知MC=ME,所以M到A、C的距離之和MA+MC=MA+ME,又MA+ME大于等于AE,所以當MA+ME=AE時,M到A、C的距離之和最小,此時A、M、E成一條直線,M點是直線AE與在x軸的交點.
所以設直線AE的解析式為![]() ,把A(4,8)和E(2,-4)代入
,把A(4,8)和E(2,-4)代入![]() 得:
得:
![]() ,
,
解得:![]() ,
,
所以直線AE的解析式為![]() ,令
,令![]() 得
得![]() ,
,
所以點M的坐標為(![]() ,0).
,0).


 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在三角形ABC中,D是BC上一點,且∠CDA=∠CAB.(注:三角形內角和等于180°)

(1)求證:∠CDA=∠DAB+∠DBA;
(2)如圖2,MN是經過點D的一條直線,若直線MN交AC邊于點E,且∠CDE=∠CAD.求證:∠AED+∠EAB=180°;
(3)將圖2中的直線MN繞點D旋轉,使它與射線AB交于點P(點P不與點A,B重合).在圖3中畫出直線MN,并用等式表示∠CAD,∠BDP,∠BPD這三個角之間的數量關系,不需證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:點A、B在數軸上分別表示有理數a、b,A、B兩點之間的距離表示為AB,在數軸上A、B兩點之間的距離AB=|a﹣b|.回答下列問題:
(1)數軸上表示﹣3和1兩點之間的距離是 ,數軸上表示﹣2和3的兩點之間的距離是 ;
(2)數軸上表示x和﹣1的兩點之間的距離表示為 ;
(3)若x表示一個有理數,則|x﹣2|+|x+3|有最小值嗎?若有,請求出最小值;若沒有,請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某興趣小組為了了解本校男生參加課外體育鍛煉情況,隨機抽取本校300名男生進行了問卷調查,統計整理并繪制了如下兩幅尚不完整的統計圖.
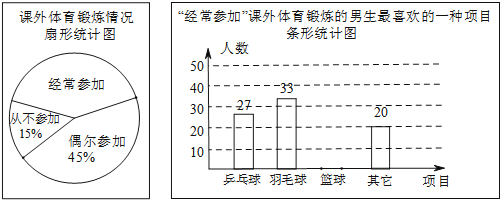
請根據以上信息解答下列問題:
![]() 課外體育鍛煉情況扇形統計圖中,“經常參加”所對應的圓心角的度數為______;
課外體育鍛煉情況扇形統計圖中,“經常參加”所對應的圓心角的度數為______;
![]() 請補全條形統計圖;
請補全條形統計圖;
![]() 該校共有1200名男生,請估計全校男生中經常參加課外體育鍛煉并且最喜歡的項目是籃球的人數;
該校共有1200名男生,請估計全校男生中經常參加課外體育鍛煉并且最喜歡的項目是籃球的人數;
![]() 小明認為“全校所有男生中,課外最喜歡參加的運動項目是乒乓球的人數約為
小明認為“全校所有男生中,課外最喜歡參加的運動項目是乒乓球的人數約為![]() ”,請你判斷這種說法是否正確,并說明理由.
”,請你判斷這種說法是否正確,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知矩形ABCD的三個頂點![]() 、
、![]() 、
、![]() 拋物線
拋物線![]() 過A、C兩點.
過A、C兩點.
![]() 直接寫出點A的坐標,并求出拋物線的解析式;
直接寫出點A的坐標,并求出拋物線的解析式;
![]() 動點P從點A出發
動點P從點A出發![]() 沿線段AB向終點B運動,同時點Q從點C出發,沿線段CD向終點D運動
沿線段AB向終點B運動,同時點Q從點C出發,沿線段CD向終點D運動![]() 速度均為每秒1個單位長度,運動時間為t秒
速度均為每秒1個單位長度,運動時間為t秒![]() 過點P作
過點P作![]() 交AC于點E.
交AC于點E.
![]() 過點E作
過點E作![]() 于點F,交拋物線于點
于點F,交拋物線于點![]() 當t為何值時,線段EG最長?
當t為何值時,線段EG最長?
![]() 連接
連接![]() 在點P、Q運動的過程中,判斷有幾個時刻使得
在點P、Q運動的過程中,判斷有幾個時刻使得![]() 是等腰三角形?請直接寫出相應的t值.
是等腰三角形?請直接寫出相應的t值.

查看答案和解析>>
科目:初中數學 來源: 題型:
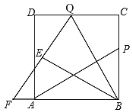
【題目】如圖,P為邊長為6的正方形ABCD的邊BC上一動點(P與B、C不重合),Q在CD上,且CQ=BP,連接AP、BQ,將△BQC沿BQ所在的直線翻折得到△BQE,延長QE交BA的延長線于點F.
(1)試探究AP與BQ的數量與位置關系,并證明你的結論;
(2)當E是FQ的中點時,求BP的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
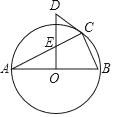
【題目】如圖,△ABC內接于⊙O,且AB為⊙O的直徑OD⊥AB,與AC交于點E,與過點C的⊙O切線交于點D.
(1)若AC=6,BC=3,求OE的長.
(2)試判斷∠A與∠CDE的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形ABCD中,AB=3,BC=4,點E是BC邊上一點,連接AE,把∠B沿AE折疊,使點B落在點B′處,當△CEB′為直角三角形時,BE的長為( )
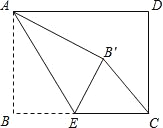
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】躍壯五金商店準備從寧云機械廠購進甲、乙兩種零件進行銷售.若每個甲種零件的進價比每個乙種零件的進價少2元,且用80元購進甲種零件的數量與用100元購進乙種零件的數量相同.
(1)求每個甲種零件、每個乙種零件的進價分別為多少元?
(2)若該五金商店本次購進甲種零件的數量比購進乙種零件的數量的3倍還少5個,購進兩種零件的總數量不超過95個,該五金商店每個甲種零件的銷售價格為12元,每個乙種零件的銷售價格為15元,則將本次購進的甲、乙兩種零件全部售出后,可使銷售兩種零件的總利潤(利潤=售價-進價)超過371元,通過計算求出躍壯五金商店本次從寧云機械廠購進甲、乙兩種零件有幾種方案?請你設計出來.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com