【題目】如圖，在四邊形ABCD中，AB=BC，對角線BD平分ABC，P是BD上一點，過點P作PM^AD，PN^CD，垂足分別為M、N。
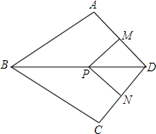
（1）求證：ADB=CDB；
（2）若ADC=90°，求證：四邊形MPND是正方形。
【答案】見解析
【解析】
試題（1）根據角平分線的性質和全等三角形的判定方法證明△ABD≌△CBD，由全等三角形的性質即可得到：∠ADB=∠CDB；
（2）若∠ADC=90°，由（1）中的條件可得四邊形MPND是矩形，再根據兩邊相等的四邊形是正方形即可證明四邊形MPND是正方形．
證明：（1）∵對角線BD平分∠ABC，
∴∠ABD=∠CBD，
在△ABD和△CBD中，
，
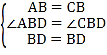∴△ABD≌△CBD（SAS），
∴∠ADB=∠CDB；
（2）∵PM⊥AD，PN⊥CD，
∴∠PMD=∠PND=90°，
∵∠ADC=90°，
∴四邊形MPND是矩形，
∵∠ADB=∠CDB，
∴∠ADB=45°
∴PM=MD，
∴四邊形MPND是正方形．
同步練習強化拓展系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線y=ax2+bx+c（a≠0）的對稱軸為直線x=﹣1，且拋物線經過A（1，0），C（0，3）兩點，與x軸交于點B．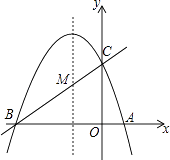
（1）若直線y=mx+n經過B、C兩點，求直線BC和拋物線的解析式；
（2）在拋物線的對稱軸x=﹣1上找一點M，使點M到點A的距離與到點C的距離之和最小，求出點M的坐標；
（3）設點P為拋物線的對稱軸x=﹣1上的一個動點，求使△BPC為直角三角形的點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】根據題意結合圖形填空：如圖，
點
在
上，點
在
上，
，
.試說明：∥.將過程補充完整.
解：∵（已知）
且
（ ）
∴
（等量代換）
∴ ∥ （ ）
∴
（ ）
又∵（已知）
∴ = （等量代換 ）
∴∥（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
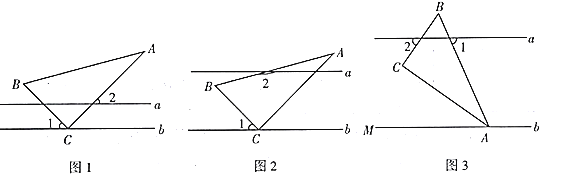
【題目】在綜合與實踐課上，同學們以“一個含
的直角三角尺和兩條平行線”為背景開展數學活動，如圖，已知兩直線
且
和直角三角形
，
，
，
.
操作發現：
（1）在如圖1中，
，求
的度數；
（2）如圖2，創新小組的同學把直線
向上平移，并把的位置改變，發現
，說明理由；
實踐探究：
（3）縝密小組在創新小組發現結論的基礎上，將如圖中的圖形繼續變化得到如圖，
平分
，此時發現
與又存在新的數量關系，請直接寫出與的數量關系.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“PM2.5”指數是空氣中可入肺顆粒物的含量，是空氣質量的指標之一．下表為A市1﹣12月“PM2.5月平均指數”（單位：微克/立方米）
PM2.5指數 | 20 | 30 | 40 | 41 | 43 | 50 |
月數 | 2 | 4 | 3 | 1 | 1 | 1 |
（1）求這12個月“PM2.5月平均指數”的眾數、中位數、平均數；
（2）根據《環境空氣質量標準》，宜居城市的標準之一是“PM2.5年平均指數少于35微克/立方米”，請你判斷A市是否為宜居城市？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在安慶市第三屆中小學生道路交通安全網絡知識競賽活動中，某中學的老師要求同學們都參加社會實踐活動，一天，王明和張強兩位同學到市中心的廣場的十字路口，觀察、統計上午7：
：00中闖紅燈的人次，制作了如下的兩個數據統計圖
井且提出了一些問題
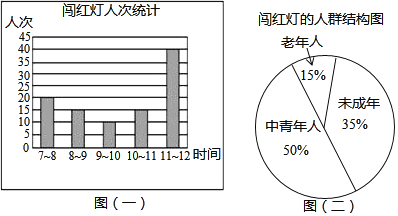
求圖
一
提供的五個數據各時段闖紅燈人次的平均數并說明這兩幅統計圖各有什么特點？
估計一個月按30天計算上午7：：00在該十字路口闖紅燈的未成年人約有多少人次？
請你根據統計圖提供的信息向交通管理部門提出一條合理化建議．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“一帶一路”國際合作高峰論壇于5月14日在北京開幕，學校在初三年級隨機抽取了50名同學進行“一帶一路”知識競答，并將他們的競答成績繪制成如圖的條形統計圖，本次知識競答成績的中位數是分．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在5×5的正方形網格中，每個小正方形的邊長為1，請在所給網格中按下列要求畫出圖形.
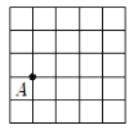
（1）已知點A在格點（即小正方形的頂點）上，畫一條線段AB，長度為
，且點B在格點上.
（2）以上題所畫的線段AB為一邊，另外兩條邊長分別為
，
. 畫一個△ABC，使點C在格點上（只需畫出符合條件的一個三角形）.
（3）所畫出的△ABC的邊AB上的高線長為 .（直接寫出答案）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AD∥BC，BE平分∠ABC交AD于點E，BD平分∠EBC．
（1）若∠DBC=35°，則∠A的度數為________；
（2）若∠DBC=α，求∠A的度數（用含α的代數式表示）；
（3）已知120°<∠ABC<180°，若點F在線段AE上，連接BF，當△BFD為直角三角形時，求∠A與∠FBE的數量關系．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com