
【題目】用“☆”定義一種新運算:對于任意有理數a和b,規定a☆b=ab2﹣2ab+b.
如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27
(1)求(﹣4)☆7的值;
(2)若(1﹣3x)☆(﹣4)=32,求x的值.
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某公司需要購買甲、乙兩種商品共150件,甲、乙兩種商品的價格分別為600元和1000元![]() 且要求乙種商品的件數不少于甲種商品件數的2倍
且要求乙種商品的件數不少于甲種商品件數的2倍![]() 設購買甲種商品x件,購買兩種商品共花費y元.
設購買甲種商品x件,購買兩種商品共花費y元.
![]() 請求出y與x的函數關系式及x的取值范圍.
請求出y與x的函數關系式及x的取值范圍.
![]() 試利用函數的性質說明,當購買多少件甲種商品時,所需要的費用最少?
試利用函數的性質說明,當購買多少件甲種商品時,所需要的費用最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠一周計劃每日生產自行車100輛,由于工人實行輪休,每日上班人數不一定相等,實際每日生產量與計劃量相比情況如下表(以計劃量為標準,增加的車輛數記為正數,減少的車輛數記為負數):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減/輛 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
(1)生產量最多的一天比生產量最少的一天多生產多少輛?
(2)本周總的生產量是多少輛?比原計劃是增加(或減少)了多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數學興趣小組想測量電線桿AB的高度,他們發現電線桿的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD與地面成30°角,且此時測得高1 m的標桿的影長為2 m,則電線桿的高度為________m(結果保留根號).
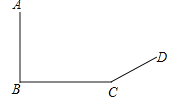
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長度為1個單位長度的小正方形組成的正方形中,點A、B、C在小正方形的頂點上.
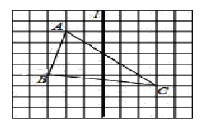
(1)在圖中畫出與△ABC關于直線l成軸對稱的△A′B′C′;
(2)三角形ABC的面積為 ;
(3)以AC為邊作與△ABC全等的三角形(頂點在格點上,不包括△ABC),可作出 個;
(4)在直線l上找一點P,使PA+PB的長最短.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=20cm,點P從點A出發,沿AB以2cm/s的速度勻速向終點B運動;同時點Q從點B出發,沿BA以4cm/s的速度勻速向終點A運動,設運動時間為ts
(1)填空:PA= cm;BQ= cm;(用含t的代數式表示)
(2)當P、Q兩點相遇時,求t的值;
(3)探究:當PQ兩點相距5cm時,求t的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,O是AB上一點, ⊙O與BC相切于點E,交AB于點F,連接AE,若AF=2BF,則∠CAE的度數是__.
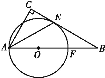
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,PA,PB,DE切⊙O于點A,B,C,D在PA上,E在PB上,
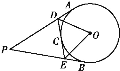
(1)若PA=10,求△PDE的周長;
(2)若∠P=50°,求∠O的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
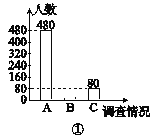
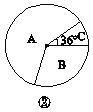
【題目】為了了解初中生畢業后就讀普通高中或就讀中等職業技術學校的意向,某校對八、九年級部分學生進行了一次調查,調查結果有三種情況:A.只愿意就讀普通高中;B.只愿意就讀中等職業技術學校;C.就讀普通高中或中等職業技術學校都愿意.學校教務處將調查數據進行了整理,并繪制了如圖25-3-3所示的尚不完整的統計圖,請根據相關信息,解答下列問題:
(1)本次活動共調查了多少名學生?
(2)補全圖①,并求出圖②中B區域的圓心角的度數;
(3)若該校八、九年級的學生共有2800名,請估計該校八、九年級學生中只愿意就讀中等職業技術學校的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com