
【題目】小飛研究二次函數y=-(x-m)2-m+1(m為常數)性質時如下結論:①這個函數圖象的頂點始終在直線y=-x+1上;②存在一個m的值,使得函數圖象的頂點與![]() 軸的兩個交點構成等腰直角三角形;③點A(x1,y1)與點B(x2,y2)在函數圖象上,若x1<x2,x1+x2>2m,則y1<y2;④當-1<x<2時,y隨x的增大而增大,則m的取值范圍為m≥2其中錯誤結論的序號是( )
軸的兩個交點構成等腰直角三角形;③點A(x1,y1)與點B(x2,y2)在函數圖象上,若x1<x2,x1+x2>2m,則y1<y2;④當-1<x<2時,y隨x的增大而增大,則m的取值范圍為m≥2其中錯誤結論的序號是( )
A. ①B. ②C. ③D. ④
【答案】C
【解析】
把頂點坐標代入y=-x+1即可判斷①;根據勾股定理即可判斷②;根據在對稱軸的右邊y隨x的增大而減小可判斷③;;根據在對稱軸的右邊y隨x的增大而增大可判斷④.
把(m,-m+1)代入y=-x+1,-m+1=-m+1,左=右,故①正確;
當-(x-m)2-m+1=0時,x1=![]() , x2=
, x2=![]() ,
,
若頂點與![]() 軸的兩個交點構成等腰直角三角形,
軸的兩個交點構成等腰直角三角形,
則1-m+(1-m)2+1-m+(1-m)2=4(1-m),即m2-m=0,
∴m=0或1時,∴存在一個m的值,使得函數圖象的頂點與![]() 軸的兩個交點構成等腰直角三角形;故②正確;
軸的兩個交點構成等腰直角三角形;故②正確;
當x1<x2,且x1、x2在對稱軸右側時,
∵-1<0, ∴在對稱軸右側y隨x的增大而減小,即y1>y2,故③錯誤;
∵-1<0, ∴在對稱軸左側y隨x的增大而增大,
∴m≥2,故④正確.
故選C.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,Rt△ABC的頂點分別是A(﹣3,2)B(0,4)C(0,2).
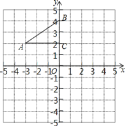
(1)將△ABC以點C為旋轉中心旋轉180°,畫出旋轉后對應的△A1B1C1;
(2)分別連接AB1,BA1后,求四邊形AB1A1B的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣有A、B兩個大型蔬菜基地,共有蔬菜700噸.若將A基地的蔬菜全部運往甲市所需費用與B基地的蔬菜全部運往甲市所需費用相同.從A、B兩基地運往甲、乙兩市的運費單價如下表:
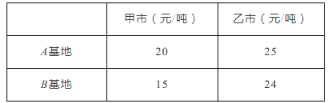
(1)求A、B兩個蔬菜基地各有蔬菜多少噸?
(2)現甲市需要蔬菜260噸,乙市需要蔬菜440噸.設從A基地運送![]() 噸蔬菜到甲市,請問怎樣調運可使總運費最少?
噸蔬菜到甲市,請問怎樣調運可使總運費最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
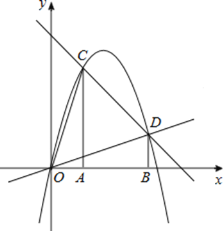
【題目】如圖,過![]() 、
、![]() 作x軸的垂線,分別交直線
作x軸的垂線,分別交直線![]() 于C、D兩點
于C、D兩點![]() 拋物線
拋物線![]() 經過O、C、D三點.
經過O、C、D三點.
![]() 求拋物線的表達式;
求拋物線的表達式;
![]() 點M為直線OD上的一個動點,過M作x軸的垂線交拋物線于點N,問是否存在這樣的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形?若存在,求此時點M的橫坐標;若不存在,請說明理由;
點M為直線OD上的一個動點,過M作x軸的垂線交拋物線于點N,問是否存在這樣的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形?若存在,求此時點M的橫坐標;若不存在,請說明理由;
![]() 若
若![]() 沿CD方向平移
沿CD方向平移![]() 點C在線段CD上,且不與點D重合
點C在線段CD上,且不與點D重合![]() ,在平移的過程中
,在平移的過程中![]() 與
與![]() 重疊部分的面積記為S,試求S的最大值.
重疊部分的面積記為S,試求S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A在拋物線y=3x2-2x+2上運動.過點A作AC⊥x軸于點C,以AC為對角線作矩形ABCD,連結BD,則對角線BD的最小值為_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對某一個函數給出如下定義:如果存在常數![]() ,對于任意的函數值
,對于任意的函數值![]() ,都滿足
,都滿足![]() ≤
≤![]() ,那么稱這個函數是有上界函數;在所有滿足條件的
,那么稱這個函數是有上界函數;在所有滿足條件的![]() 中,其最小值稱為這個函數的上確界.例如,函數
中,其最小值稱為這個函數的上確界.例如,函數![]() ,
, ![]() ≤2,因此是有上界函數,其上確界是2.如果函數
≤2,因此是有上界函數,其上確界是2.如果函數![]() (
(![]() ≤x≤
≤x≤![]() ,
, ![]() <
<![]() )的上確界是
)的上確界是![]() ,且這個函數的最小值不超過2
,且這個函數的最小值不超過2![]() ,則
,則![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() ≤
≤![]() B.
B. ![]() C.
C. ![]() ≤
≤![]() D.
D. ![]() ≤
≤![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市茶葉專賣店銷售某品牌茶葉,其進價為每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后來經過市場調查發現,單價每降低 10 元,則平均每周的銷售量可增加 40 千克,若該專賣店銷售這種品牌茶葉要想平均每周獲利 41600 元,請回答:
(1)每千克茶葉應降價多少元?
(2)在平均每周獲利不變的情況下,為盡可能讓利于顧客,贏得市場,該店應按原售價的 幾折出售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,已知∠C=90°,∠B=55°,點D在邊BC上,BD=2CD.把線段BD 繞著點D逆時針旋轉α(0<α<180)度后,如果點B恰好落在Rt△ABC的邊上,那么α=__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD 中,AB=4,AD=a,點P在AD上,且AP=2,點E是邊AB上的動點,以PE為邊作直角∠EPF,射線PF交BC于點F,連接EF,給出下列結論:①tan∠PFE=![]() ;②a的最小值為10.則下列說法正確的是( )
;②a的最小值為10.則下列說法正確的是( )
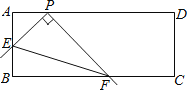
A.①②都對B.①②都錯C.①對②錯D.①錯②對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com