
【題目】小聰在用描點法畫二次函數(shù)y=ax2+bx+c![]() 的圖象時,列出下面的表格:
的圖象時,列出下面的表格:
x | … | -5 | -4 | -3 | -2 | -1 | … |
y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
根據(jù)表格提供的信息,下列說法錯誤的是( ).
A. 該拋物線的對稱軸是直線x=-2![]()
B. b2-4ac>0![]()
C. 該拋物線與y![]() 軸的交點坐標(biāo)為(0,-3.5)
軸的交點坐標(biāo)為(0,-3.5)
D. 若(0.5,y1)![]() 是該拋物線上一點.則y1<-2.5
是該拋物線上一點.則y1<-2.5![]()
 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,分別以![]() 的直角邊AC及斜邊AB向外作等邊
的直角邊AC及斜邊AB向外作等邊![]() ,等邊
,等邊![]() .已知∠BAC=30°,EF⊥AB,垂足為F,連結(jié)DF.試說明AC=EF;
.已知∠BAC=30°,EF⊥AB,垂足為F,連結(jié)DF.試說明AC=EF;

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分別找一點M,N,使△AMN周長最小時,則∠AMN+∠ANM的度數(shù)是________

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
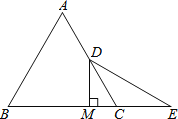
【題目】如圖:已知等邊△ABC中,D是AC的中點,E是BC延長線上的一點,且CE=CD,DM⊥BC,垂足為M,
(1)求證:M是BE的中點.
(2)若CD=1,DE=![]() ,求△ABD的周長.
,求△ABD的周長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】八(1)班組織了一次食品安全知識競賽,甲、乙兩隊各5人的成績?nèi)绫硭?/span>(10分制).
數(shù)據(jù) | 中位數(shù) | 眾數(shù) | 方差 | |||||
甲 | 8 | 10 | 9 | 6 | 9 | 9 | 1.84 | |
乙 | 10 | 8 | 9 | 7 | 8 | 8 | 1.04 | |
(1)補全表格中的眾數(shù)和中位數(shù)
(2)并判斷哪隊的成績更穩(wěn)定?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
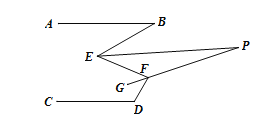
【題目】(10分)如圖下圖所示,已知AB//CD, ∠B=30°,∠D=120°;

(1)若∠E=60°,則∠E=______;
(2)請?zhí)剿鳌螮與∠F之間滿足的數(shù)量關(guān)系?說明理由.
(3)如下圖所示,已知EP平分∠BEF,FG平分∠EFD,反向延長FG交EP于點P,求∠P的度數(shù);
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】△ABC在平面直角坐標(biāo)系中的位置如圖所示.
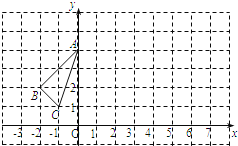
(1)畫出△ABC關(guān)于y軸對稱的△A1B1C1;
(2)將△ABC向右平移6個單位,作出平移后的△A2B2C2,并寫出△A2B2C2各頂點的坐標(biāo);
(3)觀察△A1B1C1和△A2B2C2,它們是否關(guān)于某條直線對稱?若是,請在圖上畫出這條對稱軸.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖①,在平面直角坐標(biāo)系中,點![]() 、
、![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,
軸上,![]() 軸,
軸,![]() .點
.點![]() 從
從![]() 點出發(fā),以1cm/s的速度沿邊
點出發(fā),以1cm/s的速度沿邊![]() 勻速運動,點
勻速運動,點![]() 從點
從點![]() 出發(fā),沿線段
出發(fā),沿線段![]() 勻速運動.點
勻速運動.點![]() 與點
與點![]() 同時出發(fā),其中一點到達(dá)終點,另一點也隨之停止運動.設(shè)點
同時出發(fā),其中一點到達(dá)終點,另一點也隨之停止運動.設(shè)點![]() 運動的時間為
運動的時間為![]() (s),
(s),![]() 的面積為
的面積為![]() (cm2),己知
(cm2),己知![]() 與
與![]() 之間的函數(shù)關(guān)系如圖②中的曲線段
之間的函數(shù)關(guān)系如圖②中的曲線段![]() 、線段
、線段![]() 與曲線段
與曲線段![]() .
.


(1)點![]() 的運動速度為 cm/s,點
的運動速度為 cm/s,點![]() 的坐標(biāo)為 ;
的坐標(biāo)為 ;
(2)求曲線![]() 段的函數(shù)解析式;
段的函數(shù)解析式;
(3)當(dāng)![]() 為何值時,
為何值時,![]() 的面積是四邊形
的面積是四邊形![]() 的面積的
的面積的![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將1、![]() 、
、![]() 、
、![]() 按如圖方式排列,若規(guī)定(m、n)表示第m排從左向右第n個數(shù),則(6,5)與(13,6)表示的兩數(shù)之積是( )
按如圖方式排列,若規(guī)定(m、n)表示第m排從左向右第n個數(shù),則(6,5)與(13,6)表示的兩數(shù)之積是( )

A.![]() B.6C.
B.6C.![]() D.
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com