

 ③HP//AE ④HF=1 ⑤
③HP//AE ④HF=1 ⑤
| A.2個 | B.3個 | C.4個 | D.5個 |
 則可證明M為AB中等,故Rt△AEM≌Rt△BEM,則AE=BE。
則可證明M為AB中等,故Rt△AEM≌Rt△BEM,則AE=BE。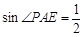 正確:因為正方形ABCD中,E為CD中點,所以Rt△ADE中,AD=2DE,所以
正確:因為正方形ABCD中,E為CD中點,所以Rt△ADE中,AD=2DE,所以 ,所以
,所以
 ,但∠EPA并不等于90°,所以②不正確;
,但∠EPA并不等于90°,所以②不正確;

 NE=2,
NE=2, PM,故可得HF=
PM,故可得HF=




科目:初中數學 來源:不詳 題型:單選題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
 ,∠B=45°.直角三角板含45°角的頂點E在邊BC上移動,一直角邊始終經過點A,斜邊與CD交于點F,若△ABE是以AB為腰的等腰三角形,則CF= .
,∠B=45°.直角三角板含45°角的頂點E在邊BC上移動,一直角邊始終經過點A,斜邊與CD交于點F,若△ABE是以AB為腰的等腰三角形,則CF= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com