【題目】如圖，將一個長方形放置在平面直角坐標系中，
，點
是
的中點，反比例函數圖像過點且和
相交于點
.
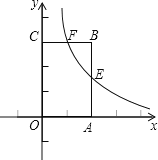
（1）求直線
和反比例函數的解析式；
（2）求四邊形
的面積.
【答案】（1）直線OB的解析式是y＝
x．反比例函數的解析式是y＝
；（2）3.
【解析】
（1）根據OA=2，OC=3，得到點B的坐標，再進一步運用待定系數法求直線OB的解析式，根據E是AB的中點，求得點E的坐標，再進一步運用待定系數法求得反比例函數的解析式；
（2）根據反比例函數的解析式求得點F的橫坐標，再進一步根據四邊形的面積等于矩形的面積減去兩個直角三角形的面積進行計算．
（1）由題意得B（2，3），E(2，)，
設直線OB的解析式是y=k1x，
把B點坐標代入，得k1=，
則直線OB的解析式是y＝x．
設反比例函數解析式是y＝
，
把E點坐標代入，得k2=3，
則反比例函數的解析式是y＝；
（2）由題意得Fy=3，代入y＝，
得Fx=1，即F（1，3）．
則四邊形OEBF的面積=矩形OABC的面積-△OAE的面積-△OCF的面積=6-3=3．
精英口算卡系列答案科目：初中數學 來源： 題型：
【題目】如圖，五邊形ABCDE中，∠A＝140°，∠B＝120°，∠E＝90°，CP和DP分別是∠BCD、∠EDC的外角平分線，且相交于點P，則∠CPD＝__________°．
查看答案和解析>>
科目：初中數學 來源： 題型：
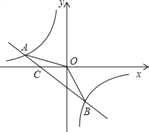
【題目】如圖，已知A（–4，n），B（2，–4）是一次函數y=kx+b的圖象和反比例函數
的圖象的兩個交點．
（1）求反比例函數和一次函數的解析式；
（2）求直線AB與x軸的交點C的坐標及△AOB的面積；
（3）求不等式
的解集（請直接寫出答案）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y＝k1x(x≥0)與雙曲線y＝
(x＞0)相交于點P(2，4)．已知點A(4，0)，B(0，3)，連接AB，將Rt△AOB沿OP方向平移，使點O移動到點P，得到△A′PB′.過點A′作A′C∥y軸交雙曲線于點C，連接CP.
(1)求k1與k2的值；
(2)求直線PC的解析式；
(3)直接寫出線段AB掃過的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠AOB=90°，將三角尺的直角頂點P落在∠AOB的平分線OC的任意一點上，使三角尺的兩條直角邊與∠AOB的兩邊分別相交于點E、F。證明：PE=PF。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，給出五個等量關系：①AD＝BC；②AC＝BD；③CE＝DE；④∠D＝∠C；⑤∠DAB＝∠CBA．
請你以其中兩個為條件，另外三個中的一個為結論，推出一個正確的結論（只需寫出一種情況），并加以證明．
已知：
求證：
證明：
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
