
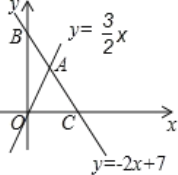
【題目】如圖,直線y=﹣2x+7與x軸、y軸分別相交于點C、B,與直線y=![]() x相交于點A.
x相交于點A.
(1)求A點坐標;
(2)求△OAC的面積;
(3)如果在y軸上存在一點P,使△OAP是以OA為底邊的等腰三角形,求P點坐標;
(4)在直線y=﹣2x+7上是否存在點Q,使△OAQ的面積等于6?若存在,請求出Q點的坐標,若不存在,請說明理由.
【答案】(1)A點坐標是(2,3);(2)![]() =
=![]() ;(3)P點坐標是(0,
;(3)P點坐標是(0, ![]() );(4)點Q是坐標是(
);(4)點Q是坐標是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
解析
聯立方程,解方程即可求得;
C點位直線y=﹣2x+7與x軸交點,可得C點坐標為(![]() ,0),由(1)得A點坐標,可得
,0),由(1)得A點坐標,可得![]() 的值;
的值;
(3)設P點坐標是(0,y),根據勾股定理列出方程,解方程即可求得;
(4)分兩種情況:①當Q點在線段AB上:作QD⊥y軸于點D,則QD=x,根據
![]() =
=![]() -
-![]() 列出關于x的方程解方程求得即可;②當Q點在AC的延長線上時,作QD⊥x軸于點D,則QD=-y,根據
列出關于x的方程解方程求得即可;②當Q點在AC的延長線上時,作QD⊥x軸于點D,則QD=-y,根據![]() =
=![]() -
- ![]() 列出關于y的方程解方程求得即可.
列出關于y的方程解方程求得即可.
解(1)解方程組: 得:
得:![]() ,
,
![]() A點坐標是(2,3);
A點坐標是(2,3);
(2)![]() C點位直線y=﹣2x+7與x軸交點,可得C點坐標為(
C點位直線y=﹣2x+7與x軸交點,可得C點坐標為(![]() ,0)
,0)
![]()
![]() =
=![]() =
=![]()
(3)設P點坐標是(0,y ),
![]() △OAP是以OA為底邊的等腰三角形,
△OAP是以OA為底邊的等腰三角形,
![]() OP=PA,
OP=PA,
![]()
![]() ,
,
解得y=![]() ,
,
![]() P點坐標是(0,
P點坐標是(0, ![]() ),
),
故答案為(0, ![]() );
);
(4)存在;
由直線y=-2x+7可知B(0,7),C(![]() ,0),
,0),
![]()
![]() =
=![]() =
=![]() <6,
<6,
![]() =
=![]() =7>6,
=7>6,
![]() Q點有兩個位置:Q在線段AB上和AC的延長線上,設點Q的坐標是(x,y),
Q點有兩個位置:Q在線段AB上和AC的延長線上,設點Q的坐標是(x,y),
當Q點在線段AB上:作QD⊥y軸于點D,如圖1, 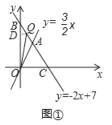
則QD=x,![]()
![]() =
=![]() -
-![]() =7-6=1,
=7-6=1,
![]()
![]() OB
OB![]() QD=1,即:
QD=1,即: ![]()
![]() 7x=1,
7x=1,
![]() x=
x=![]() ,
,
把x=![]() 代入y=-2x+7,得y=
代入y=-2x+7,得y=![]() ,
,
![]() Q的坐標是(
Q的坐標是(![]() ,
,![]() ),
),
當Q點在AC的延長線上時,作QD⊥x軸于點D,如圖2
則QD=-y,
![]()
![]() =
=![]() -
- ![]() =6-
=6-![]() =
=![]() ,
,
![]()
![]() OC
OC![]() QD=
QD=![]() ,即:
,即:![]() ,
,
![]() y=-
y=-![]() ,
,
把y=-![]() 代入y=-2x+7,解得x=
代入y=-2x+7,解得x=![]()
![]() Q的坐標是(
Q的坐標是(![]() ,-
,-![]() ),
),
綜上所述:點Q是坐標是(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度數.
請完善解答過程,并在括號內填寫相應的理論依據.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代換)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性質)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1為北京城市女生從出生到15歲的平均身高統計圖,圖2是北京城市某女生從出生到12歲的身高統計圖. 
請你根據以上信息預測該女生15歲時的身高約為 , 你的預測理由是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,PA切⊙O于點A,PO交⊙O于點C,連接BC,∠P=∠B. 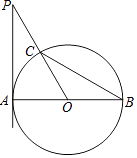
(1)求∠P的度數;
(2)連接PB,若⊙O的半徑為a,寫出求△PBC面積的思路. 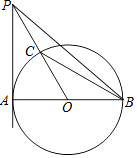
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖用點A(3,1)表示放置3個胡蘿卜、1棵青菜,點B(2,3)表示放置2個胡蘿卜、3棵青菜.

(1)請你寫出其他各點C,D,E,F所表示的意義;
(2)若一只兔子從A到達B(順著方格線走),有以下幾條路可以選擇:①A→C→D→B;②A→F→D→B;③A→F→E→B,幫可愛的小白兔選一條路,使它吃到的食物最多.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數 y=(m﹣2)x+3﹣m 的圖象不經過第三象限,且 m 為正整數.
(1)求 m 的值.
(2)在給出的平面直角坐標系中畫出該一次函數的圖象.
(3)當﹣4<y<0 時,根據函數圖象,求 x 的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
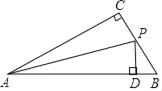
【題目】如圖,在面積為6的Rt△ABC中,∠C=90°,AC=4,AB=5,BC邊上有一動點P,當點P到AB邊的距離等于PC的長時,那么點P到端點B的距離等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,反比例函數y= ![]() (x>0)的圖象與矩形OABC對角線的交點為M,分別與AB,BC交于點D,E,連接OD,OE,則
(x>0)的圖象與矩形OABC對角線的交點為M,分別與AB,BC交于點D,E,連接OD,OE,則 ![]() = , 當k=4時,四邊形ODBE的面積為平方單位.
= , 當k=4時,四邊形ODBE的面積為平方單位. 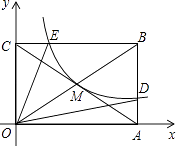
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com