
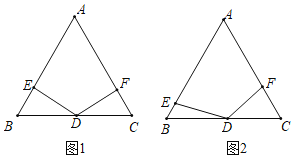
【題目】在等邊三角形ABC中,點D是BC的中點,點E、F分別是邊AB、AC(含線段AB、AC的端點)上的動點,且∠EDF=120°,小明和小慧對這個圖形展開如下研究:
問題初探:
(1)如圖1,小明發現:當∠DEB=90°時,BE+CF=nAB,則n的值為______;
問題再探:
(2)如圖2,在點E、F的運動過程中,小慧發現兩個有趣的結論:
①DE始終等于DF;②BE與CF的和始終不變;請你選擇其中一個結論加以證明.
成果運用
(3)若邊長AB=4,在點E、F的運動過程中,記四邊形DEAF的周長為L,L=DE+EA+AF+FD,則周長L的變化范圍是______.
【答案】(1)![]() ;(2)BE與CF的和始終不變,見解析;(3)
;(2)BE與CF的和始終不變,見解析;(3)![]()
【解析】
(1)先利用等邊三角形判斷出BD=CD=![]() AB,進而判斷出BE=
AB,進而判斷出BE=![]() BD,再判斷出∠DFC=90°,得出CF=
BD,再判斷出∠DFC=90°,得出CF=![]() CD,即可得出結論;
CD,即可得出結論;
(2)①構造出△EDG≌△FDH(ASA),得出DE=DF,即可得出結論;
②由(1)知,BG+CH=![]() AB,由①知,△EDG≌△FDH(ASA),得出EG=FH,即可得出結論;
AB,由①知,△EDG≌△FDH(ASA),得出EG=FH,即可得出結論;
(3)由(1)(2)判斷出L=2DE+6,再判斷出DE⊥AB時,L最小,點F和點C重合時,DE最大,即可得出結論.
解:(1)∵△ABC是等邊三角形,
∴∠B=∠C=60°,AB=BC,
∵點D是BC的中點,
∴BD=CD=![]() BC=
BC=![]() AB,
AB,
∵∠DEB=90°,
∴∠BDE=90°-∠B=30°,
在Rt△BDE中,BE=![]() BD,
BD,
∵∠EDF=120°,∠BDE=30°,
∴∠CDF=180°-∠BDE-∠EDF=30°,
∵∠C=60°,
∴∠DFC=90°,
在Rt△CFD中,CF=![]() CD,
CD,
∴BE+CF=![]() BD+
BD+![]() CD=
CD=![]() BC=
BC=![]() AB,
AB,
∵BE+CF=nAB,
∴n=![]() ,
,
故答案為![]() ;
;
(2)如圖2
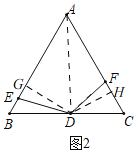
①過點D作DG⊥AB于G,DH⊥AC于H,
∴∠DGB=∠AGD=∠CFD=∠AHF=90°,
∵△ABC是等邊三角形,
∴∠A=60°,
∴∠GDH=360°-∠AGD-∠AHD-∠A=120°,
∵∠EDF=120°,
∴∠EDG=∠FDH,
∵△ABC是等邊三角形,且D是BC的中點,
∴∠BAD=∠CAD,
∵DG⊥AB,DH⊥AC,
∴DG=DH,
在△EDG和△FDH中,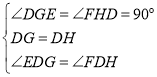 ,
,
∴△EDG≌△FDH(ASA),
∴DE=DF,
即:DE始終等于DF;
②同(1)的方法得,BG+CH=![]() AB,
AB,
由①知,△EDG≌△FDH(ASA),
∴EG=FH,
∴BE+CF=BG-EG+CH+FH=BG+CH=![]() AB,
AB,
∴BE與CF的和始終不變
(3)由(2)知,DE=DF,BE+CF=![]() AB,
AB,
∵AB=4,
∴BE+CF=2,
∴四邊形DEAF的周長為L=DE+EA+AF+FD
=DE+AB-BE+AC-CF+DF
=DE+AB-BE+AB+DE
=2DE+2AB-(BE+CF)
=2DE+2×4-2
=2DE+6,
∴DE最大時,L最大,DE最小時,L最小,
當DE⊥AB時,DE最小,
由(1)知,BG=![]() BD=1,
BD=1,
∴DE最小=![]() BG=
BG=![]() ,
,
∴L最小=2![]() +6,
+6,
當點F和點C重合時,DE最大,此時,∠BDE=180°-∠EDF=120°=60°,
∵∠B=60°,
∴∠B=∠BDE=∠BED=60°,
∴△BDE是等邊三角形,
∴DE=BD=![]() AB=2,
AB=2,
即:L最大=2×2+6=10,
∴周長L的變化范圍是2![]() ≤L≤10,
≤L≤10,
故答案為2![]() ≤L≤10.
≤L≤10.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
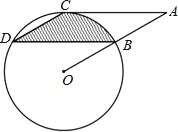
【題目】如圖,點B、C、D都在⊙O上,過點C作AC∥BD交OB延長線于點A,連接CD,且∠CDB=∠OBD=30°,DB=![]() cm.
cm.
(1)求證:AC是⊙O的切線;
(2)求由弦CD、BD與弧BC所圍成的陰影部分的面積.(結果保留π)
查看答案和解析>>
科目:初中數學 來源: 題型:
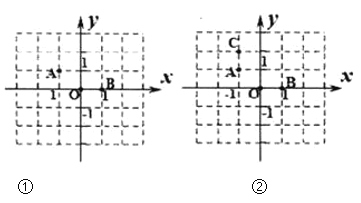
【題目】在棋盤中建立如圖①所示的平面直角坐標系,二顆棋子![]() 、
、![]() 、
、![]() 的位置如圖,它們的坐標分別為
的位置如圖,它們的坐標分別為![]() 、
、![]() 、
、![]() .
.
(1)如圖②,添加棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 為端點的四條首尾連接的線段圍成的圖形成為軸對稱圖形,請在圖中畫出該圖形的對稱軸;
為端點的四條首尾連接的線段圍成的圖形成為軸對稱圖形,請在圖中畫出該圖形的對稱軸;
(2)在其它格點位置添加一顆棋子![]() ,使
,使![]() 、
、![]() 、
、![]() 、
、![]() 為端點的首尾連接的四條線段構成一個軸對稱圖形,請直接寫出點
為端點的首尾連接的四條線段構成一個軸對稱圖形,請直接寫出點![]() 的坐標。(寫山2個即可)
的坐標。(寫山2個即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為滿足市場需求,某超市在五月初五“端午節”來臨前夕,購進一種品牌
粽子,每盒進價是40元,超市規定每盒售價不得少于45元.根據以往銷售經驗發現:當售價定為每盒45元時,每天可賣出700盒,每盒售價每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價![]() (元)之間的函數關系式;(4分)
(元)之間的函數關系式;(4分)
(2)當每盒售價定為多少元時,每天銷售的利潤![]() (元)最大?最大利潤是多少?(6分)
(元)最大?最大利潤是多少?(6分)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,∠BAC=![]() (
(![]() ),將線段BC繞點B逆時針旋轉60°得到線段BD。
),將線段BC繞點B逆時針旋轉60°得到線段BD。

(1)如圖1,直接寫出∠ABD的大小(用含![]() 的式子表示);
的式子表示);
(2)如圖2,∠BCE=150°,∠ABE=60°,判斷△ABE的形狀并加以證明;
(3)在(2)的條件下,連結DE,若∠DEC=45°,求![]() 的值。
的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
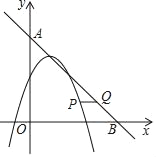
【題目】定義:對于給定的二次函數y=a(x﹣h)2+k(a≠0),其伴生一次函數為y=a(x﹣h)+k,例如:二次函數y=2(x+1)2﹣3的伴生一次函數為y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函數y=(x﹣1)2﹣4,則其伴生一次函數的表達式為_____;
(2)試說明二次函數y=(x﹣1)2﹣4的頂點在其伴生一次函數的圖象上;
(3)如圖,二次函數y=m(x﹣1)2﹣4m(m≠0)的伴生一次函數的圖象與x軸、y軸分別交于點B、A,且兩函數圖象的交點的橫坐標分別為1和2,在∠AOB內部的二次函數y=m(x﹣1)2﹣4m的圖象上有一動點P,過點P作x軸的平行線與其伴生一次函數的圖象交于點Q,設點P的橫坐標為n,直接寫出線段PQ的長為![]() 時n的值.
時n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點O,過點O作EF∥BC交AB于E,交AC于F,過點O作OD⊥AC于D,下列四個結論:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③點O到△ABC各邊的距離相等;
④設OD=m,AE+AF=n,則S△AEF=mn.
其中正確的結論是( )

A.①②③B.①②④C.②③④D.①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com