
【題目】用一條長為18的繩子圍成一個等腰三角形.
(1)若等腰三角形有一條邊長為4,它的其它兩邊是多少?
(2)若等腰三角形的三邊長都為整數,請直接寫出所有能圍成的等腰三角形的腰長.
【答案】(1)其他兩邊分別為4和7;(2)y=2時,x=8,y=4時,x=7,y=8時,x=5.
【解析】
(1)根據等腰三角形的性質即可求出答案.
(2)設等腰三角形的三邊長為x、x、y,根據題意可知y<9,y是2的倍數,從而可求出答案.
解:(1)當等腰三角形的腰長為4,
∴底邊長為18﹣4×2=10,
∵4+4<10,
∴4、4、10不能組成三角形,
當等腰三角形的底邊長為4,
∴腰長為(18﹣4)÷2=7,
∵4+7>7,
∴4、7、7能組成三角形,
綜上所述,其他兩邊分別為4和7.
(2)設等腰三角形的三邊長為x、x、y,
由題意可知:2x+y=18,
且2x>y,
∴y<9,
∵x=![]() =9﹣
=9﹣![]() ,x與y都是整數,
,x與y都是整數,
∴y是2的倍數,
∴y=2時,x=8,
y=4時,x=7,
y=8,x=5.


科目:初中數學 來源: 題型:
【題目】(10分)水果店張阿姨以每斤2元的價格購進某種水果若干斤,然后以每斤4元的價格出售,每天可售出100斤,通過調查發現,這種水果每斤的售價每降低0.1元,每天可多售出20斤,為保證每天至少售出260斤,張阿姨決定降價銷售.
(1)若將這種水果每斤的售價降低x元,則每天的銷售量是 斤(用含x的代數式表示);
(2)銷售這種水果要想每天盈利300元,張阿姨需將每斤的售價降低多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,G是邊長為8的正方形ABCD的邊BC上的一點,矩形DEFG的邊EF過點A,GD=10.
(1)求FG的長;
(2)直接寫出圖中與△BHG相似的所有三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,BC=CD,E,F,G,H分別為AB,BC,CD,AD的中點,順次連接E,G,F,H,求證:四邊形EFGH是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,有以下結論:①abc>0,②a﹣b+c<0,③2a+b=0,④b2﹣4ac>0,其中正確結論個數是( )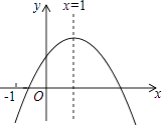
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣ ![]() x+6分別交x軸、y軸于A、B兩點,拋物線y=﹣
x+6分別交x軸、y軸于A、B兩點,拋物線y=﹣ ![]() x2+8,與y軸交于點D,點P是拋物線在第一象限部分上的一動點,過點P作PC⊥x軸于點C.
x2+8,與y軸交于點D,點P是拋物線在第一象限部分上的一動點,過點P作PC⊥x軸于點C.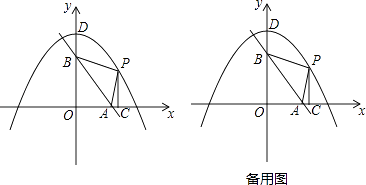
(1)點A的坐標為 , 點D的坐標為;
(2)探究發現:
①假設P與點D重合,則PB+PC=;(直接填寫答案)
②試判斷:對于任意一點P,PB+PC的值是否為定值?并說明理由;
(3)試判斷△PAB的面積是否存在最大值?若存在,求出最大值,并求出此時點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在ABCD中,AE平分∠BAD交BC邊于E,EF⊥AE交CD于F.
(1)求證:CE=CF;
(2)延長AD、EF交于點H,延長BA到G,使AG=CF,若AD=7,DF=3,EH=2AE,求GF的長.
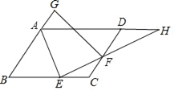
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD中,AB=10cm,BC=8cm,CD=12cm,∠B=∠C,點E為AB的中點.如果點P在線段BC上以3cm/s的速度沿B-C-B運動,同時,點Q在線段CD上由C點向D點運動.當點Q的運動速度為_______cm/s時,能夠使△BPE≌△CQP.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com