Question

【題目】如圖，已知ΔABC內接于⊙O，AB為⊙O的直徑，BD⊥AB，交AC的延長線于點D．

（1）若E是BD的中點，連結CE，試判斷CE與⊙O的位置關系．

（2）若AC=3CD，求∠A的大小．

Answer 1

【答案】（1）位置關系：CE是⊙O的切線；（2）30°.

【解析】分析：（1）連接OC，利用思路：連半徑，通過角的變換，證明出CO與CE的垂直關系，即可得出結論。（2）用m表示出DC、AC，根據△ACB∽△BCD，得出一組等量關系，從而求出BC，再求出∠A的正切值，即可得出∠A=30。

詳解：（1）位置關系：CE是⊙O的切線.

連接OC，

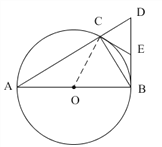
∵AB是⊙O的直徑，

∴∠ACB=∠DCB=90°.

∵點E是BD的中點，

∴BE=CE.

∴∠EBC=∠ECB.

∵OC=OB

∴∠OCB=∠OBC

∴∠ECB+∠OCB=∠EBC+∠OBC

∴∠OCE=∠OBE.

∵BD⊥AB

∴∠OCE=∠OBE=90°

∴CE是⊙O的切線.

（2）∵∠ACB=∠BCD，∠A=∠DBC

∴ΔACB∽ΔBCD.

∴

∴

∵AC=3CD

∴,即

∴在RtΔACB中,tan∠A=

∴∠A=30°.