
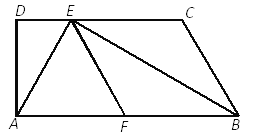
【題目】如圖,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于點E,F是AB的中點,聯結AE、EF,且AE⊥BE.
求證:(1)四邊形BCEF是菱形;
(2)![]() .
.
【答案】(1)證明見解析;(2)證明見解析.
【解析】分析:(1)根據角平分線的性質可得出∠ABE=∠CBE,由直角三角形斜邊上中線等于斜邊的一半可得出EF=BF=![]() AB,進而可得出∠FEB=∠FBE=∠CBE,由“內錯角相等,兩直線平行”可得出EF∥BC,結合AB∥CD可得出四邊形BCEF是平行四邊形,再由鄰邊EF=BF即可證出四邊形BCEF是菱形;
AB,進而可得出∠FEB=∠FBE=∠CBE,由“內錯角相等,兩直線平行”可得出EF∥BC,結合AB∥CD可得出四邊形BCEF是平行四邊形,再由鄰邊EF=BF即可證出四邊形BCEF是菱形;
(2)根據菱形的性質可得出BC=BF,結合BF=![]() AB可得出AB=2BC,由AB∥CD可得出∠DEA=∠EAB,結合∠D=∠AEB=90°可證出△EDA∽△AEB,根據相似三角形的性質可得出BEAE=ADBA,代入BA=2BC即可證出結論.
AB可得出AB=2BC,由AB∥CD可得出∠DEA=∠EAB,結合∠D=∠AEB=90°可證出△EDA∽△AEB,根據相似三角形的性質可得出BEAE=ADBA,代入BA=2BC即可證出結論.
詳解:(1)∵BE平分∠ABC,∴∠ABE=∠CBE.
∵AE⊥BE,∴∠AEB=90°.
∵F是AB的中點,∴EF=BF=![]() AB,∴∠FEB=∠FBE=∠CBE,∴EF∥BC.
AB,∴∠FEB=∠FBE=∠CBE,∴EF∥BC.
∵AB∥CD,∴四邊形BCEF是平行四邊形.
∵EF=BF,∴四邊形BCEF是菱形.
(2)∵四邊形BCEF是菱形,∴BC=BF.
∵BF=![]() AB,∴AB=2BC.
AB,∴AB=2BC.
∵AB∥CD,∴∠DEA=∠EAB.
∵∠D=∠AEB=90°,∴△EDA∽△AEB,∴![]() =
=![]() ,∴BEAE=ADBA,∴BEAE=2ADBC.
,∴BEAE=ADBA,∴BEAE=2ADBC.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】A、B、C為數軸上的三點,動點A、B同時從原點出發,動點A每秒運動x個單位,動點B每秒運動y個單位,且動點A運動到的位置對應的數記為a,動點B運動到的位置對應的數記為b,定點C對應的數為8.
(1)若2秒后,a、b滿足|a+8|+|b﹣2|=0,則x= ,y= .并請在數軸上標出A、B兩點的位置.
(2)若動點A、B在(1)運動后的位置上保持原來的速度,且同時向正方向運動z秒后使得|a|=|b|,使得z= .
(3)若動點A、B在(1)運動后的位置上都以每秒2個單位向正方向運動繼續運動t秒,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC,點A與點B之間的距離為AB,且AC+BC=1.5AB,則t= .
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
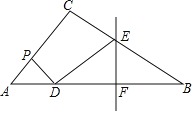
【題目】如圖,在△ABC中,∠C=![]() ,點P在AC上運動,點D在AB上,PD始終保持與PA相等,BD的垂直平分線交BC于點E,交BD于點F,連接DE.若AC=6,BC=8,PA=2,則線段DE的長為________
,點P在AC上運動,點D在AB上,PD始終保持與PA相等,BD的垂直平分線交BC于點E,交BD于點F,連接DE.若AC=6,BC=8,PA=2,則線段DE的長為________
查看答案和解析>>
科目:初中數學 來源: 題型:
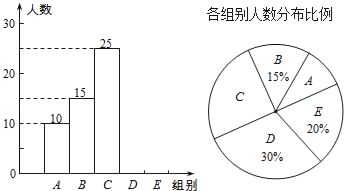
【題目】某校舉行全體學生“漢字聽寫”比賽,每位學生聽寫漢字39個.隨機抽取了部分學生的聽寫結果,繪制成如下的圖表.
組別 | 正確字數x | 人數 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根據以上信息完成下列問題:
(1)統計表中的m= ,n= ,并補全條形統計圖;
(2)扇形統計圖中“C組”所對應的圓心角的度數是 ;
(3)已知該校共有900名學生,如果聽寫正確的字的個數少于24個定為不合格,請你估計該校本次聽寫比賽不合格的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
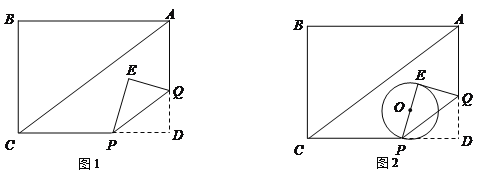
【題目】如圖1,在矩形ABCD中,AD=3,DC=4,動點P在線段DC上以每秒1個單位的速度從點D向點C運動,過點P作PQ∥AC交AD于Q,將△PDQ沿PQ翻折得到△PQE. 設點P的運動時間為t(s).
(1)當點E落在邊AB上時,t的值為 ;
(2)設△PQE與△ADC重疊部分的面積為s,求s與t的函數關系式;
(3)如圖2,以PE為直徑作⊙O.當⊙O與AC邊相切時,求CP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司招聘職員,對甲、乙兩位候選人進行了面試,面試中包括形體、口才、專業知識,他們的成績(百分制)如下表:

(1)如果公司根據經營性質和崗位要求,以面試成績中形體、口才、專業知識按照![]() 的比值確定成績,請計算甲、乙兩人各自的平均成績,看看誰將被錄取?
的比值確定成績,請計算甲、乙兩人各自的平均成績,看看誰將被錄取?
(2)如果公司根據經營性質和崗位要求,以面試成績中形體占![]() ,口才占
,口才占![]() ,專業知識占
,專業知識占![]() 確定成績,那么你認為該公司應該錄取誰?
確定成績,那么你認為該公司應該錄取誰?
查看答案和解析>>
科目:初中數學 來源: 題型:
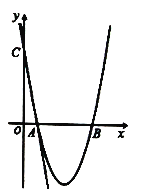
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 兩點,拋物線
兩點,拋物線![]() 經過
經過![]() 兩點,與
兩點,與![]() 軸交于另一點
軸交于另一點![]() .
.
(1)求拋物線解析式及![]() 點坐標;
點坐標;
(2)連接![]() ,求
,求![]() 的面積;
的面積;
(3)若點![]() 為拋物線上一動點,連接
為拋物線上一動點,連接![]() ,當點
,當點![]() 運動到某一位置時,
運動到某一位置時,![]() 面積為
面積為![]() 的面積的
的面積的![]() 倍,求此時點
倍,求此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有兩點A、B,點B在點A的右側,且AB=10,點A表示的數為﹣6.動點P從點A出發,以每秒4個單位長度的速度沿數軸向右勻速運動.
(1)寫出數軸上點B表示的數;
(2)經過多少時間,線段AP和BP的長度之和為18?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
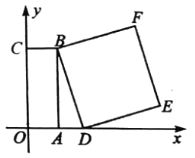
【題目】如圖,以矩形![]() 的頂點
的頂點![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立平面直角坐標系.已知,
軸,建立平面直角坐標系.已知,![]() ,
,![]() ,點
,點![]() 為
為![]() 軸上一動點,以
軸上一動點,以![]() 為一邊在
為一邊在![]() 右側作正方形
右側作正方形![]() .
.
(1)若點![]() 與點
與點![]() 重合,請直接寫出點
重合,請直接寫出點![]() 的坐標.
的坐標.
(2)若點![]() 在
在![]() 的延長線上,且
的延長線上,且![]() ,求點
,求點![]() 的坐標.
的坐標.
(3)若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com