
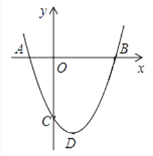
【題目】已知:如圖,拋物線的頂點(diǎn)D的坐標(biāo)為(1,-4),且與y軸交于點(diǎn)C(0,-3).
(1)求該函數(shù)的關(guān)系式及該拋物線與x軸的交點(diǎn)A,B的坐標(biāo).
(2)請直接寫出△ABC的外心M的坐標(biāo).
(3)點(diǎn)E為該拋物線上一動(dòng)點(diǎn),且滿足tan∠ABE=![]() tan∠ACB,請求出點(diǎn)E的坐標(biāo).
tan∠ACB,請求出點(diǎn)E的坐標(biāo).
【答案】(1)![]() ,A(-1,0) B(3,0);(2) (1,-1);(3)(-
,A(-1,0) B(3,0);(2) (1,-1);(3)(-![]() ),(-
),(-![]() ,-
,-![]() ).
).
【解析】
(1)利用頂點(diǎn)式即可解決問題,令y=0,解方程即可得到A、B的坐標(biāo);
(2)由外心為三邊中垂線的交點(diǎn),得到外心M在拋物線的對稱軸x=1上,設(shè)M(1,y),根據(jù)MA=MC,用兩點(diǎn)間的距離公式列方程,求解即可;
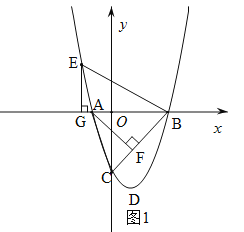
(3)連接AC、BC.過A作AF⊥CB于F.先求出tan∠ACB的值,即可得到tan∠ABE的值.分兩種情況討論:①當(dāng)E在x軸上方時(shí),如圖1,過E作EG⊥x軸于G,連接EB.設(shè)E(x,x2-2x-3),則EG= x2-2x-3,GB=3-x,由tan∠ABE=![]() ,列方程求出x的值,即可得到E的坐標(biāo);②當(dāng)E在x軸上方時(shí),如圖2,同理可求E的坐標(biāo).
,列方程求出x的值,即可得到E的坐標(biāo);②當(dāng)E在x軸上方時(shí),如圖2,同理可求E的坐標(biāo).
(1)設(shè)拋物線頂點(diǎn)式為y=a(x﹣1)2-4,將C(0,-3)代入得:a-4=-3,解得:a=1,所以拋物線的關(guān)系式為:y=(x﹣1)2﹣4=x2-2x-3,令y=0,即:(x﹣1)2﹣4=0,解得:x1=3,x2=﹣1.∴坐標(biāo)為A(﹣1,0),B(3,0).
(2)∵外心為三邊中垂線的交點(diǎn),∴外心M在拋物線的對稱軸x=1上,設(shè)M(1,y).
∵MA=MC,∴![]() ,解得:y=-1,∴M(1,-1);
,解得:y=-1,∴M(1,-1);
(3)連接AC、BC.過A作AF⊥CB于F.AB=3-(-1)=4,BC=![]() .
.
∵OB=OC=3,∴∠OBC=45°,∴AF=BF=![]() ,∴CF=BC-BF=
,∴CF=BC-BF=![]() ,∴tan∠ACB=
,∴tan∠ACB=![]() =2,∴tan∠ABE=
=2,∴tan∠ABE=![]() tan∠ACB=
tan∠ACB=![]() ./span>
./span>
分兩種情況討論:①當(dāng)E在x軸上方時(shí),如圖1,過E作EG⊥x軸于G,連接EB.設(shè)E(x,x2-2x-3),則EG= x2-2x-3,GB=3-x.
∵tan∠ABE=![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),∴x=
(舍去),∴x=![]() ,y= x2-2x-3=
,y= x2-2x-3=![]() ,∴E(
,∴E(![]() ,
,![]() );
);
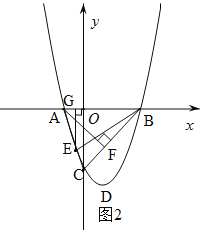
②當(dāng)E在x軸上方時(shí),如圖2,過E作EG⊥x軸于G,連接EB.設(shè)E(x,x2-2x-3),則EG= -x2+2x+3,GB=3-x.
∵tan∠ABE=![]() ,∴
,∴![]() ,∴
,∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),∴x=
(舍去),∴x=![]() ,y= x2-2x-3=
,y= x2-2x-3=![]() ,∴E(
,∴E(![]() ,
,![]() ).
).
綜上所述:E的坐標(biāo)為(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 贏在課堂名師課時(shí)計(jì)劃系列答案
贏在課堂名師課時(shí)計(jì)劃系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
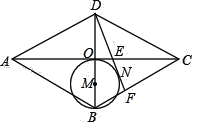
【題目】如圖,在菱形ABCD中,對角線AC、BD交于點(diǎn)O,以OB為直徑畫圓M,過D作⊙M的切線,切點(diǎn)為N,分別交AC、BC于點(diǎn)E、F,已知AE=5,CE=3,則菱形ABCD的面積是( )
A. 24B. 20C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某通訊公司推出①,②兩種通訊收費(fèi)方式供用戶選擇,其中一種有月租費(fèi),另一種無月租費(fèi),且兩種收費(fèi)方式的通訊時(shí)間x(分)與費(fèi)用y(元)之間的函數(shù)關(guān)系如圖所示.
(1)有月租的收費(fèi)方式是________(填“①”或“②”),月租費(fèi)是________元;
(2)分別求出①,②兩種收費(fèi)方式中y與自變量x之間的函數(shù)表達(dá)式;
(3)請你根據(jù)用戶通訊時(shí)間的多少,給出經(jīng)濟(jì)實(shí)惠的選擇建議.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)A、D、C、F在同一條直線上,AD=CF,AB=DE,BC=EF.
(1)求證:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度數(shù).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商場一種商品的進(jìn)價(jià)為每件30元,售價(jià)為每件40元.每天可以銷售48件,為盡快減少庫存,商場決定降價(jià)促銷.
(1)若該商品連續(xù)兩次下調(diào)相同的百分率后售價(jià)降至每件32.4元,求兩次下降的百分率;
(2)經(jīng)調(diào)查,若每降價(jià)0.5元,每天可多銷售4件,那么每天要想獲得510元的利潤,每件應(yīng)降價(jià)多少元?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,在平面直角坐標(biāo)系xOy中,等邊△AOB的邊長為6,點(diǎn)C在邊OA上,點(diǎn)D在邊AB上,且OC=3BD,反比例函數(shù)![]() (k≠0)的圖象恰好經(jīng)過點(diǎn)C和點(diǎn)D,則k的值為( )
(k≠0)的圖象恰好經(jīng)過點(diǎn)C和點(diǎn)D,則k的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
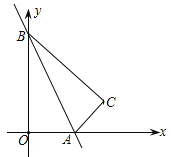
【題目】如圖,一次函數(shù)的圖象與x軸、y軸分別相交于點(diǎn)A、B,將△AOB沿直線AB翻折,得△ACB.若C(![]() ,
,![]() ),則該一次函數(shù)的解析式為 .
),則該一次函數(shù)的解析式為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)揚(yáng)州市某風(fēng)景區(qū)的旅游信息,![]() 公司組織一批員工到該風(fēng)景區(qū)旅游,支付給旅行社
公司組織一批員工到該風(fēng)景區(qū)旅游,支付給旅行社![]() 元.
元. ![]() 公司參加這次旅游的員工有多少人?
公司參加這次旅游的員工有多少人?
揚(yáng)州市某風(fēng)景區(qū)旅游信息表
旅游人數(shù) | 收費(fèi)標(biāo)準(zhǔn) |
不超過 | 人均收費(fèi) |
超過 | 每增加 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com