
【題目】如圖,在△ABC中,BC的垂直平分線交它的外接圓于D、E兩點.若∠B=24°,∠C=106°,則![]() 的度數為____
的度數為____
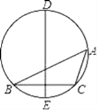
【答案】82°
【解析】
根據垂徑定理的推理可判斷DE為直徑,根據垂徑定理得到![]() ,設△ABC的外接圓的圓心為O,連結OC、OA,如圖,再利用三角形內角和計算出∠BAC=50°,利用圓周角定理得到∠EOC=∠BAC=50°,∠AOC=2∠B=48°,然后計算出∠AOD的度數,再根據
,設△ABC的外接圓的圓心為O,連結OC、OA,如圖,再利用三角形內角和計算出∠BAC=50°,利用圓周角定理得到∠EOC=∠BAC=50°,∠AOC=2∠B=48°,然后計算出∠AOD的度數,再根據![]() 的度數等于它所對的圓心角的度數求解即可.
的度數等于它所對的圓心角的度數求解即可.
解:∵DE垂直平分BC,
∴DE為直徑,![]() ,
,
設△ABC的外接圓的圓心為O,連結OC、OA,如圖,
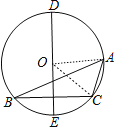
∵∠B=24°,∠C=106°,
∴∠BAC=180°-24°-106°=50°,
∴∠EOC=∠BAC=50°,
∵∠AOC=2∠B=48°,
∴∠AOD=180°-∠COE-∠AOC=180°-50°-48°=82°,
∴![]() 的度數為82°.
的度數為82°.
故答案為82°.


科目:初中數學 來源: 題型:
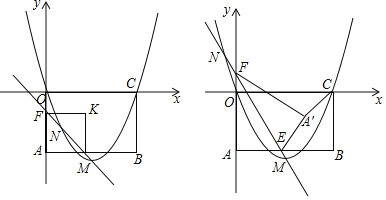
【題目】矩形OABC的邊OC、OA分別位于x、y軸上,點A(0,﹣4)、B(6,﹣4)、C(6,0),拋物線y=ax2+bx經過點O和點C,頂點M(3,﹣![]() ),點N是拋物線上一動點,直線MN交直線AB于點E,交y軸于F,△A′EF是將△AEF沿直線MN翻折后的圖形.
),點N是拋物線上一動點,直線MN交直線AB于點E,交y軸于F,△A′EF是將△AEF沿直線MN翻折后的圖形.
(1)求拋物線的解析式;
(2)當四邊AEA′F是正方形時,求點N的坐標.
(3)連接CA′,求CA′的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
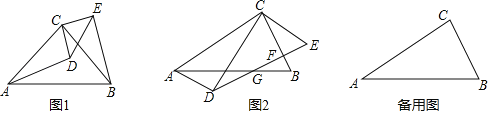
【題目】(1)△ABC和△CDE是兩個等腰直角三角形,如圖1,其中∠ACB=∠DCE=90°,連結AD、BE,求證:△ACD≌△BCE.
(2)△ABC和△CDE是兩個含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE從邊CD與AC重合開始繞點C逆時針旋轉一定角度α(0°<α<180°);
①如圖2,DE與BC交于點F,與AB交于點G,連結AD,若四邊形ADEC為平行四邊形,求![]() 的值;
的值;
②若AB=10,DE=8,連結BD、BE,當以點B、D、E為頂點的三角形是直角三角形時,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.其中卷第九“勾股”章,主要講述了以測量問題為中心的直角三角形三邊互求的關系.其中記載:“今有邑,東西七里,南北九里,各中開門,出東門一十五里有木,問:出南門幾何步而見木?”譯文:“如圖,今有一座長方形小城,東西向城墻長7里,南北向城墻長9里,各城墻正中均開一城門.走出東門15里處有棵大樹,問走出南門多少步恰好能望見這棵樹?”(注:1里=300步)你的計算結果是:出南門________步而見木.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】東北大米主要種植于黑龍江省、吉林省、遼寧省的廣大平原地區,種植在極其肥沃的黑土地中,吸收了足夠的氮、磷、鉀等多種礦物元素,陽光雨露充足,又有純凈無污染的灌溉用水,生長周期比較長,一般五個月左右.東北大米顆粒飽滿,質地堅硬,色澤清白透明;飯粒油亮,香味濃郁;蒸煮后出飯率高,粘性較小,米質較脆.劉阿姨到超市購買東北大米,第一次按原價購買,用了105元.幾天后,遇上這種大米8折出售,她用140元又買了一些,兩次共購買了40kg.這種東北大米的原價是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是平行四邊形,對角線
是平行四邊形,對角線![]() 在
在![]() 軸正半軸上,位于第一象限的點
軸正半軸上,位于第一象限的點![]() 和第二象限的點
和第二象限的點![]() 分別在雙曲線
分別在雙曲線![]() 和
和![]() 的一個分支上,分別過點
的一個分支上,分別過點![]() 作
作![]() 軸的垂線段,垂足分別為點
軸的垂線段,垂足分別為點![]() 和
和![]() ,則以下結論:
,則以下結論:
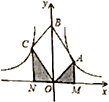
①![]() ; ②陰影部分面積是
; ②陰影部分面積是![]() ;
;
③當![]() 時,
時,![]() ; ④若
; ④若![]() 是菱形,則兩雙曲線既關于x軸對稱,也關于y軸對稱.
是菱形,則兩雙曲線既關于x軸對稱,也關于y軸對稱.
其中正確結論的個數是
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸正半軸相交于A、B兩點,與y軸相交于點C,對稱軸為直線x=2,且OA=OC,則下列結論:①abc>0;②9a+3b+c<0;③c>﹣1;④關于x的方程ax2+bx+c=0(a≠0)有一個根為![]() ,其中正確結論的個數為( )
,其中正確結論的個數為( )
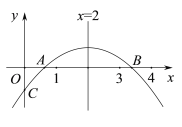
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com