
【題目】如圖,已知正方形ABCD,AB=3,點E在線段AB上,AE=1連結DE,DE的垂直平分線交DE于點P,交DC的延長線于點Q,PQ交BC于點G,連結EQ,EQ交BC于點F,連結GE.
(1)求證:△ADE∽△PQD;
(2)求線段CQ的長;
(3)求∠EGB的正切值.
【答案】
(1)證明:∵四邊形ABCD是正方形,
∴DC∥AB,
∴∠AED=∠PDQ,又∠DAE=∠QPD=90°,
∴△ADE∽△PQD
(2)解:由勾股定理得,DE= ![]() =
= ![]() ,
,
∵PQ是DE的垂直平分線,
∴DP= ![]() DE=
DE= ![]() ,
,
∵△ADE∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,DQ=5,
則CQ=DQ﹣DC=5﹣3=2
(3)解:由勾股定理得,PQ= ![]() =
= ![]() ,
,
∵∠QCG=∠QPD=90°,∠CQG=∠PQD,
∴△CQG∽△PQD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,CG= ![]() ,
,
∴BG=3﹣ ![]() =
= ![]() ,
,
∴tan∠EGB= ![]() =
= ![]()
【解析】(1)根據正方形的性質得到DC∥AB,得到∠AED=∠PDQ,根據兩角對應相等的兩個三角形相似證明;
(2)根據勾股定理求出DE,根據相似三角形的性質列出比例式,計算即可;
(3)根據相似三角形的性質求出CG,根據正切的概念計算即可.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對正方形的性質的理解,了解正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】補全解答過程:
已知:如圖,直線AB∥CD,直線EF與直線AB、CD分別交于點G、H,GM平分∠FGB,∠3=60°,求∠1的度數。

解:∵EF與CD交于點H(已知)
∴∠3=∠4(_______________)
∵∠3=60°(已知)
∴∠4=60°(______________)
∵AB∥CD,EF與AB、CD交于點G、H(已知)
∴∠4+∠FGB=180°(______________)
∴∠FGB=______°
∵GM平分∠FGB(已知)
∴∠1=_____°(______________)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形ABCD中剪去一個邊長為1的小正方形CEFG,動點P從點A出發,沿A→D→E→F→G→B的路線繞多邊形的邊勻速運動到點B時停止(不含點A和點B),則△ABP的面積S隨著時間t變化的函數圖象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩座城市的中心火車站A,B兩站相距360km.一列動車與一列特快列車分別從A,B兩站同時出發相向而行,動車的平均速度比特快列車快54km/h,當動車到達B站時,特快列車恰好到達距離A站135km處的C站.則動車的平均速度是 , 特快列車的平均速度是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】當三角形中一個內角是另一個內角的3倍時,我們稱此三角形為“夢想三角形”.如果一個“夢想三角形”有一個角為108°,那么這個“夢想三角形”的最小內角的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=﹣x+2的圖象與反比例函數y2= ![]() 的圖象相交于A,B兩點,與x軸相交于點C.已知tan∠BOC=
的圖象相交于A,B兩點,與x軸相交于點C.已知tan∠BOC= ![]() ,點B的坐標為(m,n).
,點B的坐標為(m,n).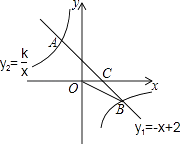
(1)求反比例函數的解析式;
(2)請直接寫出當x<m時,y2的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長度為1個單位長度的小正方形組成的正方形網格紙中,點A、B、C在小正方形的頂點上.
(1)求![]() 的面積;
的面積;
(2)在圖中畫出與![]() 關于直線1成軸對稱的
關于直線1成軸對稱的![]() ;
;
(3)在如圖所示網格紙中,以![]() 為一邊作與
為一邊作與![]() 全等的三角形,可以作出多少個三角形與
全等的三角形,可以作出多少個三角形與![]() 全等(不要超出網格紙的范圍).
全等(不要超出網格紙的范圍).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() ,
,![]() .
.
(1)在圖中畫出![]() 關于
關于![]() 軸的對稱圖形
軸的對稱圖形![]() ;
;
(2)在圖中的![]() 軸上找一點
軸上找一點![]() ,使
,使![]() 的值最小(保留作圖痕跡),并直接寫出點
的值最小(保留作圖痕跡),并直接寫出點![]() 的坐標;
的坐標;
(3)在圖中的![]() 軸上找一點
軸上找一點![]() ,使
,使![]() 的值最小(保留作圖痕跡),并直接寫出
的值最小(保留作圖痕跡),并直接寫出![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】運用“同一圖形的面積不同表示方式相同”可以證明一類含有線段的等式,這種解決問題的方法我們稱之為面積法.
(1)如圖1,在等腰三角形ABC中,AB=AC,AC邊上的高為h,M是底邊BC上的任意一點,點M到腰AB、AC的距離分別為h1、h2.請用面積法證明:h1+h2=h;

(2)當點M在BC延長線上時,h1、h2、h之間的等量關系式是 ;(直接寫出結論不必證明)
(3)如圖2在平面直角坐標系中有兩條直線l1:y=![]() x+3、l2:y=﹣3x+3,若l2上的一點M到l1的距離是1,請運用(1)、(2)的結論求出點M的坐標.
x+3、l2:y=﹣3x+3,若l2上的一點M到l1的距離是1,請運用(1)、(2)的結論求出點M的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com