【題目】如圖，已知點A、D、C、F在同一條直線上，AB=DE，BC=EF，要使△ABC≌△DEF，還需要添加一個條件是（ ）
A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
科目：初中數學 來源： 題型：
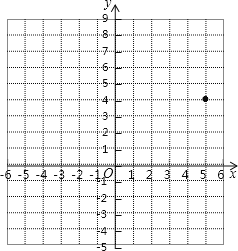
【題目】在平面直角坐標系中，A、B、C三點的坐標分別為
、
、
．
畫出
，并求的面積；
在中，點C經過平移后的對應點為
，將作同樣的平移得到
，畫出平移后的，并寫出點
，
的坐標；
已知點
為內一點，將點P向右平移4個單位后，再向下平移6個單位得到點
，則
______，
______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在甲、乙兩名同學中選拔一人參加“中華好詩詞”大賽，在相同的測試條件下，兩人5次測試成績（單位：分）如下：
甲：79，86，82，85，83
乙：88，79，90，81，72．
回答下列問題：
（1）甲成績的平均數是 ， 乙成績的平均數是；
（2）經計算知S甲2=6，S乙2=42．你認為選拔誰參加比賽更合適，說明理由；
（3）如果從甲、乙兩人5次的成績中各隨機抽取一次成績進行分析，求抽到的兩個人的成績都大于80分的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學校“瀝園文學”社成員來自初一、初二、初三三個年級的學生，其人數比為2：3：5，如圖所示的扇形圖表示上述分布情況．已知來自初一的學生為10人，則下列說法不正確的是（ ）
A. 扇形甲的圓心角是72° B. 學生的總人數是90人
C. 初三的人數比初二的人數多10人 D. 初一的人數比初三的人數少15人
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,已知一次函數y1=kx+b的圖象與反比例函數
的圖象交于A、B兩點, 且點A的坐標為（-2,3），點B的縱坐標是-2,求:
(1)一次函數與反比例函數的解析式;
（2）利用圖像指出，當
為何值時有
>
；當
為何值時有
＜
（3）利用圖像指出，當
>3時
的取值范圍。
【答案】見解析
【解析】試題分析：（1）把A點坐標代入反比例函數解析式求出m的值，把B點的縱坐標代入反比例函數解析式求出B點的橫坐標，再把A、B兩點的坐標代入一次函數解析式求出k、b的值即可；
（2）根據A、B的橫坐標，結合圖象即可得出答案；
（3）求出x＝3時y2的值，然后結合圖象即可得出y2的取值范圍．
試題解析：
解：（1）∵A（－2，3）在反比例函數y2＝
的圖象上，
∴m＝－2×3
＝－6，
即反比例函數的解析式為y2＝
．
當y2＝－2時，x＝3，
即B（3，－2），
把A（－2，3），B（3，－2）代入y＝kx＋b得：
，
解得： 
，
即一次函數的解析式為y＝－x＋1；
（2）結合圖象可得y1＞y2時對應的圖象在點A的左側和y軸與點B之間，
即x＜－2或0＜x＜3；
同理y1＜y2時對應的圖象在點A與y軸之間和點B的右側，
即－2＜x＜0或x＞3；
（3）當x＝3時，y2＝－2，
當x＞3時反比例函數對應的圖象在點B的右側部分，
對應的函數值－2＜y2＜0．
點睛：本題考查了一次函數與反比例函數的交點問題，用待定系數法求一次函數的解析式等知識點，主要考查學生的計算能力和觀察圖形的能力，用了數形結合思想．
【題型】解答題
【結束】
26
【題目】如圖，四邊形ABCD是平行四邊形，點A(1，0)，B(4，1)，C(4，4)．反比例函數
(x＞0)的圖像經過點D，點P是一次函數y=ax+4-4a(a
0)的圖像與該反比例函數圖像的一個公共點．
(1)求反比例函數的表達式；
(2)一次函數y=ax+4-4a(a
0)的圖像恒過一定點，直接寫出這個定點的坐標.
(3)對于一次函數y=ax+4-4a(a
0)，當y隨x的增大而減小時，確定點P的橫坐標的取值范圍．(不必寫出過程)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，C，D是⊙O上的點，且OC∥BD，AD分別與BC，OC相交于點E，F，則下列結論：
①AD⊥BD；②∠AOC=∠AEC；③CB平分∠ABD；④AF=DF；⑤BD=2OF；⑥△CEF≌△BED，其中一定成立的是（ ）
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，以圓O為圓心，半徑為1的弧交坐標軸于A，B兩點，P是 
上一點（不與A，B重合），連接OP，設∠POB=α，則點P的坐標是（ ）
A.（sinα，sinα）
B.（cosα，cosα）
C.（cosα，sinα）
D.（sinα，cosα）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一漁船由西往東航行，在A點測得海島C位于北偏東60°的方向，前進20海里到達B點，此時，測得海島C位于北偏東30°的方向，則海島C到航線AB的距離CD等于海里．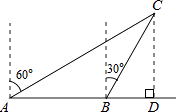
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
