
【題目】如圖,已知菱形ABCD邊長為4,![]() ,點E從點A出發沿著AD、DC方向運動,同時點F從點D出發以相同的速度沿著DC、CB的方向運動.
,點E從點A出發沿著AD、DC方向運動,同時點F從點D出發以相同的速度沿著DC、CB的方向運動.
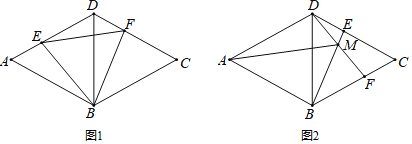
![]() 如圖1,當點E在AD上時,連接BE、BF,試探究BE與BF的數量關系,并證明你的結論;
如圖1,當點E在AD上時,連接BE、BF,試探究BE與BF的數量關系,并證明你的結論;
![]() 在
在![]() 的前提下,求EF的最小值和此時
的前提下,求EF的最小值和此時![]() 的面積;
的面積;
![]() 當點E運動到DC邊上時,如圖2,連接BE、DF,交點為點M,連接AM,則
當點E運動到DC邊上時,如圖2,連接BE、DF,交點為點M,連接AM,則![]() 大小是否變化?請說明理由.
大小是否變化?請說明理由.
【答案】![]() ,證明見解析;
,證明見解析;![]() 的最小值是
的最小值是![]() ,
,![]() ;
;![]() 如圖3,當點E運動到DC邊上時,
如圖3,當點E運動到DC邊上時,![]() 大小不發生變化,理由見解析.
大小不發生變化,理由見解析.
【解析】
![]() 先證明
先證明![]() 和
和![]() 是等邊三角形,再證明
是等邊三角形,再證明![]() ≌
≌![]() ,可得結論;
,可得結論;
![]() 由
由![]() ≌
≌![]() ,易證得
,易證得![]() 是正三角形,繼而可得當動點E運動到當
是正三角形,繼而可得當動點E運動到當![]() ,即E為AD的中點時,BE的最小,根據等邊三角形三線合一的性質可得BE和EF的長,并求此時
,即E為AD的中點時,BE的最小,根據等邊三角形三線合一的性質可得BE和EF的長,并求此時![]() 的面積;
的面積;
![]() 同理得:
同理得:![]() ≌
≌![]() ,則可得
,則可得![]() ,所以
,所以![]() ,則A、B、M、D四點共圓,可得
,則A、B、M、D四點共圓,可得![]() .
.
![]() ,
,
證明:![]() 、F的速度相同,且同時運動,
、F的速度相同,且同時運動,
![]() ,
,
又![]() 四邊形ABCD是菱形,
四邊形ABCD是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
同理![]() 也是等邊三角形,
也是等邊三角形,
![]() ,
,
在![]() 和
和![]() 中,
中,
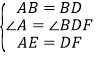 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
![]() 由
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
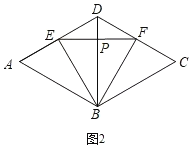
如圖2,當動點E運動到![]() ,即E為AD的中點時,BE的最小,此時EF最小,
,即E為AD的中點時,BE的最小,此時EF最小,
![]() ,
,![]() ,
,
![]() ,
,
![]() 的最小值是
的最小值是![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 如圖3,當點E運動到DC邊上時,
如圖3,當點E運動到DC邊上時,![]() 大小不發生變化,
大小不發生變化,
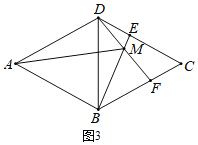
在![]() 和
和![]() 中,
中,
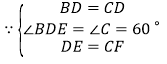 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 、B、M、D四點共圓,
、B、M、D四點共圓,
![]() .
.


科目:初中數學 來源: 題型:
【題目】計算題
(1)計算:4sin60°+|3﹣ ![]() |﹣(
|﹣( ![]() )﹣1+(π﹣2017)0 .
)﹣1+(π﹣2017)0 .
(2)先化簡,再求值:( ![]() ﹣1)÷
﹣1)÷ ![]() ,其中x的值從不等式組
,其中x的值從不等式組 ![]() 的整數解中任選一個.
的整數解中任選一個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以AB為直徑的⊙O交∠BAD的角平分線于C,過C作CD⊥AD于D,交AB的延長線于E. 
(1)求證:直線CD為⊙O的切線;
(2)當AB=2BE,且CE= ![]() 時,求AD的長.
時,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
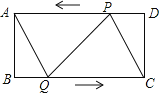
【題目】如圖,在矩形ABCD中,![]() ,
,![]() 點P從點D出發向點A運動,運動到點A即停止;同時,點Q從點B出發向點C運動,運動到點C即停止,點P、Q的速度都是
點P從點D出發向點A運動,運動到點A即停止;同時,點Q從點B出發向點C運動,運動到點C即停止,點P、Q的速度都是![]() ,連接PQ、AQ、
,連接PQ、AQ、![]() 設點P、Q運動的時間為ts.
設點P、Q運動的時間為ts.
![]() 當t為何值時,四邊形ABQP是矩形;
當t為何值時,四邊形ABQP是矩形;
![]() 當t為何值時,四邊形AQCP是菱形.
當t為何值時,四邊形AQCP是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南沙群島是我國固有領土,現在我南海漁民要在南沙某海島附近進行捕魚作業,當漁船航行至B處時,測得該島位于正北方向20(1+ ![]() )海里的C處,為了防止某國海巡警干擾,就請求我A處的漁監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.
)海里的C處,為了防止某國海巡警干擾,就請求我A處的漁監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,海中一小島有一個觀測點A,某天上午觀測到某漁船在觀測點A的西南方向上的B處跟蹤魚群由南向北勻速航行.B處距離觀測點30 ![]() 海里,若該漁船的速度為每小時30海里,問該漁船多長時間到達觀測點A的北偏西60°方向上的C處?(計算結果用根號表示,不取近似值)
海里,若該漁船的速度為每小時30海里,問該漁船多長時間到達觀測點A的北偏西60°方向上的C處?(計算結果用根號表示,不取近似值)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙上的每個小方格都是邊長為1的正方形,△ABC 的頂點均在格點上,若 B
點的坐標為(-4,-2), 按要求回答下列問題:
(1)在圖中建立正確的平面直角坐標系;
(2)根據所建立的坐標系,寫出點A和點C的坐標;
(3)畫出△ABC關于x軸的對稱圖形△ABC;
(4)△ABC 的面積為________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com