
【題目】如圖,△ABC的角平分線CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列結論:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=![]() ∠CGE.其中正確的結論是( )
∠CGE.其中正確的結論是( )

A. ②③B. ①②④C. ①③④D. ①②③④
【答案】B
【解析】
根據平行線的性質、角平分線的定義、垂直的性質及三角形內角和定理依次判斷即可得出答案.
①∵EG∥BC,
∴∠CEG=∠ACB,
又∵CD是△ABC的角平分線,
∴∠CEG=∠ACB=2∠DCB,故正確;
②∵∠A=90°,
∴∠ADC+∠ACD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC+∠BCD=90°.
∵EG∥BC,且CG⊥EG,
∴∠GCB=90°,即∠GCD+∠BCD=90°,
∴∠ADC=∠GCD,故正確;
③條件不足,無法證明CA平分∠BCG,故錯誤;
④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+![]() (∠ABC+∠ACB)=135°,
(∠ABC+∠ACB)=135°,
∴∠DFE=360°-135°-90°=135°,
∴∠DFB=45°=![]() ∠CGE,,正確.
∠CGE,,正確.
故選B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.數據4、5、5、6、0的平均數是5
B.數據2、3、4、2、3的眾數是2
C.了解某班同學的身高情況適合全面調查
D.甲、乙兩組數據的平均數相同,方差分別是S甲2=3.2,S乙2=2.9,則甲組數據更穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,過點A作GE∥BC,角平分線BD、CF相交于點H,它們的延長線分別交GE于點E、G.試在圖中找出3對全等三角形,并對其中一對全等三角形給出證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形邊長為1的網格中,點A,點C均落在格點上,點B為中點.
(Ⅰ)計算AB的長等于;
(Ⅱ)若點P,Q分別為線段BC,AC上的動點,且BP=CQ,請在如圖所示的網格中,用無刻度的直尺,畫出當PQ最短時,點P,Q的位置,并簡要說明畫圖方法(不要求證明) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,點P和Q同時從D、B出發,P由D向C運動,速度為每秒1cm,點Q由B向A運動,速度為每秒3cm,試求幾秒后,P、Q和梯形ABCD的兩個頂點所形成的四邊形是平行四邊形?
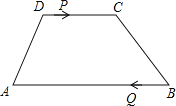
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某地方政府決定在相距50km的A、B兩站之間的公路旁E點,修建一個土特產加工基地,且使C、D兩村到E點的距離相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E應建在離A站多少千米的地方?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 ![]() 的圖象過(0,-6)、(1,0)和(-2,-6)三點.
的圖象過(0,-6)、(1,0)和(-2,-6)三點.
(1)求二次函數解析式;
(2)求二次函數圖象的頂點坐標;
(3)若點A(m-2n,-8mn-10)在此二次函數圖象上,求m、n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB =AC,AD⊥BC于點D,AM是△ABC的外角∠CAE的平分線.
(1)求證:AM∥BC;
(2)若DN平分∠ADC交AM于點N,判斷△ADN的形狀并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com