
【題目】如圖1,在四邊形ABCD中,∠DAB被對角線AC平分,且AC2=AB·AD,我們稱該四邊形為“可分四邊形”,∠DAB稱為“可分角”.
(1)如圖2,四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,如果∠DCB=∠DAB,則∠DAB=_________.
(2)如圖3,在四邊形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求證:四邊形ABCD為“可分四邊形”;
(3)現有四邊形ABCD為“可分四邊形”,∠DAB為“可分角”,且AC=4,BC=2,∠D=90°,求AD的長?

圖1 圖2 圖3
【答案】(1)![]() (2)證明見解析(3)
(2)證明見解析(3)![]()
【解析】試題分析:(1)、根據“可分四邊形”和“可分角”的定義得出答案;(2)、根據角平分線的性質得出∠DAC=∠CAB=30°,∠DCA=150°-∠ACB,然后根據角度之間的關系得出∠ADC=∠ACB,從而說明△ACD和△ABC相似,從而得出結論;(3)、根據“可分四邊形”和“可分角”的性質得出∠DAC=∠CAB, ![]() ,從而說明△ACD和△ABC相似,根據相似得出∠ACB=∠D=90°,然后根據勾股定理求出AB的長度,結合
,從而說明△ACD和△ABC相似,根據相似得出∠ACB=∠D=90°,然后根據勾股定理求出AB的長度,結合![]() 得出AD的長度.
得出AD的長度.
試題解析:(1)![]()
(2)∵AC平分∠DAB,∠DAB=60° ∴∠DAC=∠CAB=30° ∵∠DCB=150°
∴∠DCA=150°-∠ACB
在△ADC中,∠ADC=180°- ∠DAC- ∠DCA =180°-30°-(150°-∠ACB)=∠ACB
∴△ACD∽△ABC ∴![]() ∴
∴![]() , 即證四邊形ABCD為“可分四邊形”
, 即證四邊形ABCD為“可分四邊形”
(3)∵四邊形ABCD為“可分四邊形”,∠DAB為“可分角”∴AC平分∠DAB, ![]()
即∠DAC=∠CAB, ![]() ∴△ACD∽△ABC ∴∠ACB=∠D=90°
∴△ACD∽△ABC ∴∠ACB=∠D=90°
在Rt△ACB中AB= ![]() ∵
∵![]() ∴AD=
∴AD=![]()


科目:初中數學 來源: 題型:
【題目】已知,AB∥CD,AB,CD被直線l所截,點P是l上的一動點,連接PA,PC.
(1)如圖①,當P在AB,CD之間時,求證:∠APC=∠A+∠C; 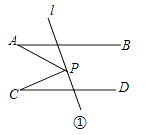
(2)如圖②,當P在射線ME上時,探究∠A,∠C,∠APC的關系并證明; 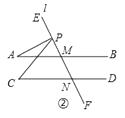
(3)如圖③,當P在射線NF上時,直接寫出∠A,∠C,∠APC三者之間關系. 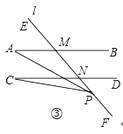
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AC=a,BD=b,且AC⊥BD,順次連接四邊形ABCD各邊中點,得到四邊形A1B1C1D1 , 再順次連接四邊形A1B1C1D1各邊中點,得到四邊形A2B2C2D2 , 如此進行下去,得到四邊形AnBnCnDn . 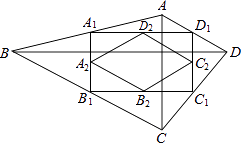
(1)求證:四邊形A1B1C1D1是矩形;
(2)四邊形A3B3C3D3是形;
(3)四邊形A1B1C1D1的周長為;
(4)四邊形AnBnCnDn的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明從二次函數y=ax2+bx+c的圖象(如圖)中觀察得出了下面五條信息:①c<0;②abc>0;③a﹣b+c>0;④2a﹣3b=0;⑤c﹣4b>0.你認為其中正確的信息是( )

A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題。
(1)如圖1,在等邊△ABC中,點M是BC上的任意一點(不含端點B、C),連結AM,以AM為邊作等邊△AMN,連結CN.求證:CN∥AB.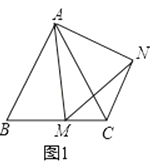
(2)如圖2,在等邊△ABC中,點M是BC延長線上的任意一點(不含端點C),其它條件不變,(1)中結論CN∥AB還成立嗎?請說明理由.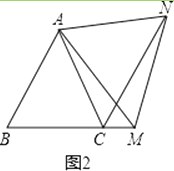
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com