
【題目】在![]() 中,以線段
中,以線段![]() 為邊作
為邊作![]() ,使得
,使得![]() ,連接
,連接![]() ,再以
,再以![]() 為邊作
為邊作![]() ,使得
,使得![]() ,
,![]() .
.
(![]() )如圖1,連結
)如圖1,連結![]() ,求證:
,求證:![]() .
.
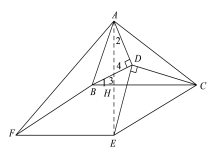
(![]() )如圖2,
)如圖2,![]() 時,將線段
時,將線段![]() 沿著射線
沿著射線![]() 的方向平移,得到線段
的方向平移,得到線段![]() ,連接
,連接![]() ,
,![]() .
.
①若![]() ,依題意補全圖2,求線段
,依題意補全圖2,求線段![]() 的長.
的長.
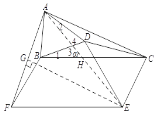
②請直接寫出線段![]() 的長(用含
的長(用含![]() 的式子表示).
的式子表示).



【答案】(![]() )證明見解析;(
)證明見解析;(![]() )①
)①![]() ,②
,②![]()
【解析】
(1)欲證明AE=BC,只要證明△ADE≌△BDC即可;
(2)①連接AE,BC于O,由△ADE≌△BDC.推出AE=BC=4,推出∠AED=∠DCB,推出四邊形BFEC為平行四邊形.推出AE=EF=4,∠AEF=90°,Rt△AEF中,根據AF=![]() ,計算即可;
,計算即可;
②作EM⊥AF于M,設AE交BC于O,DE交BC于K.由①可知△ADE≌△BDC,四邊形BCEF是平行四邊形,推出∠DCK=∠KEO,由∠DKC=∠EKO,推出∠EOK=∠CDK=α,由BC∥EF,推出∠AEF=∠EOK=α,在Rt△EFM中,FM=EFsin![]() ,可得AF=2FM=8sin
,可得AF=2FM=8sin![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,
則![]() ,
,
在![]() 和
和![]() 中,
中,
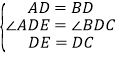 ,
,
∴![]() ≌
≌![]()
∴![]() .
.
(![]() )①連接
)①連接![]() ,設
,設![]() 交
交![]() 于
于![]() ,
,
由(![]() )
)![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 且
且![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
②連![]() ,設
,設![]() 交
交![]() 于
于![]() ,過
,過![]() 作
作![]() 于
于![]() ,
,
由(![]() )得:
)得:![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() 且
且![]() ,
,
∴![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】超市里,某商戶先后兩次購進若干千克的黃瓜,第一次用了300元,第二次用了900元,但第二次的進貨單價比第次的要高1.5元,而所購的黃瓜數量是第一次的2倍.
(1)問該商戶兩次一共購進了多少千克黃瓜?
(2)當商戶按每千克6元的價格賣掉了![]() 時,商戶想盡快賣掉這些黃瓜,于是商戶決定將剩余的黃瓜打折銷售,請你幫忙算算,剩余的黃瓜至少打幾折才能使兩次所進的黃瓜總盈利不低于360元?
時,商戶想盡快賣掉這些黃瓜,于是商戶決定將剩余的黃瓜打折銷售,請你幫忙算算,剩余的黃瓜至少打幾折才能使兩次所進的黃瓜總盈利不低于360元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年10月1日,慶祝中華人民共和國成立![]() 周年大會在京隆重舉行.當天在天安門廣場舉行了盛大閱兵式和群眾游行,閱兵式的全體受閱官兵由人民解放軍、武警部隊和民兵預備役部隊約
周年大會在京隆重舉行.當天在天安門廣場舉行了盛大閱兵式和群眾游行,閱兵式的全體受閱官兵由人民解放軍、武警部隊和民兵預備役部隊約![]() 名官兵、
名官兵、![]() 臺(套)裝備組成的
臺(套)裝備組成的![]() 個徒步方隊、
個徒步方隊、![]() 個裝備方隊;陸海、空航空兵
個裝備方隊;陸海、空航空兵![]() 余架戰機組成的
余架戰機組成的![]() 個空中梯隊和
個空中梯隊和![]() 個空中護旗隊根據上述數據繪制了以下尚不完整的統計圖表:
個空中護旗隊根據上述數據繪制了以下尚不完整的統計圖表:

根據圖表提供的信息,解答以下問題:
(1)統計表中的![]() ;
;![]() .
.
(2)請補全條形統計圖;

(3)在閱兵過程中,已知直播介紹空中護旗隊為![]() 秒,介紹每個徒步方隊裝備方隊、空中梯隊經過的時間分別為
秒,介紹每個徒步方隊裝備方隊、空中梯隊經過的時間分別為![]() 秒、
秒、![]() 秒、
秒、![]() 秒,請你求出每個方(護旗梯)隊的平均播出時間.
秒,請你求出每個方(護旗梯)隊的平均播出時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出利用尺規作圖完成下面問題:
已知:直線![]() 與直線
與直線![]() 外一點
外一點![]() .求作:過點
.求作:過點![]() 作直線
作直線![]() 的平行線.
的平行線.

已知:直線![]() 與直線
與直線![]() 外一點
外一點![]() .求作:過點
.求作:過點![]() 作直線
作直線![]() 的平行線.
的平行線.

小明的作法如下:
如圖,

①在直線![]() 上任取兩點
上任取兩點![]() ,
,![]() ;
;
②以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑作圓弧;
的長為半徑作圓弧;
以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑作圓弧;
的長為半徑作圓弧;
兩圓弧(與點![]() 在
在![]() 同側)的交點為
同側)的交點為![]() ;
;
③過點![]() ,
,![]() 作直線.
作直線.
所以直線![]() 即為所求.
即為所求.
如圖,
①在直線![]() 上任取兩點
上任取兩點![]() ,
,![]() ;
;
②以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑作圓弧;
的長為半徑作圓弧;
以點![]() 為圓心,線段
為圓心,線段![]() 的長為半徑作圓弧;
的長為半徑作圓弧;
兩圓弧(與點![]() 在
在![]() 同側)的交點為
同側)的交點為![]() ;
;
③過點![]() ,
,![]() 作直線.
作直線.
所以直線![]() 即為所求.
即為所求.
老師說:“小明的作法正確.”
請回答:(![]() )利用尺規作圖完成小明的做法(保留作圖痕跡);
)利用尺規作圖完成小明的做法(保留作圖痕跡);
(![]() )該作圖的依據是__________.
)該作圖的依據是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,AC是弦,∠BAC的平分線交⊙O于點D,過點D作DE⊥AC交AC的延長線于點E,連接BD。

(1)求證:DE是⊙O的切線;
(2)若tan∠ABD=2,CE=1,求⊙O的半徑。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知某開發區有一塊四邊形空地ABCD,現計劃在該空地上種植草皮,經測量∠ADC=90°,CD=6m,AD=8m,BC=24cm,AB=26m,若每平方米草皮需200元,則在該空地上種植草皮共需多少錢?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt![]() 中,
中,![]() ,分別以點A、C為圓心,大于
,分別以點A、C為圓心,大于![]() 長為半徑畫弧,兩弧相交于點M、N,連結MN,與AC、BC分別交于點D、E,連結AE.
長為半徑畫弧,兩弧相交于點M、N,連結MN,與AC、BC分別交于點D、E,連結AE.
(1)求![]() ;(直接寫出結果)
;(直接寫出結果)
(2)當AB=3,AC=5時,求![]() 的周長.
的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在每個小正方形的邊長為![]() 的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距
的網格圖形中,每個小正方形的頂點稱為格點.從一個格點移動到與之相距![]() 的另一個格點的運動稱為一次跳馬變換.例如,在
的另一個格點的運動稱為一次跳馬變換.例如,在![]() 的正方形網格圖形中(如圖1),從點A經過一次跳馬變換可以到達點B,C,D,E等處.現有
的正方形網格圖形中(如圖1),從點A經過一次跳馬變換可以到達點B,C,D,E等處.現有![]() 的正方形網格圖形(如圖2),則從該正方形的頂點M經過跳馬變換到達與其相對的N,最少需要跳馬變換的次數是_______,現有
的正方形網格圖形(如圖2),則從該正方形的頂點M經過跳馬變換到達與其相對的N,最少需要跳馬變換的次數是_______,現有![]() 的正方形網格圖形(如圖3),則從該正方形的頂點
的正方形網格圖形(如圖3),則從該正方形的頂點![]() 經過跳馬變換到達與其相對的
經過跳馬變換到達與其相對的![]() ,最少需要跳馬變換的次數是_______.
,最少需要跳馬變換的次數是_______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com