
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() .點
.點![]() 從
從![]() 點出發,沿
點出發,沿![]() 方向運動,以
方向運動,以![]() 為直徑作
為直徑作![]() ,當
,當![]() 運動到點
運動到點![]() 時停止運動,設
時停止運動,設![]() .
.
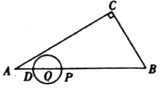
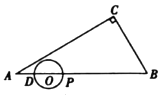
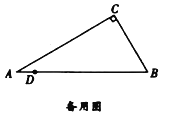
(1)![]() ___________,
___________,![]() ___________.(用
___________.(用![]() 的代數式表示)
的代數式表示)
(2)當![]() 為何值時,
為何值時,![]() 與
與![]() 的一邊相切?
的一邊相切?
(3)在點![]() 整個運動過程中,過點
整個運動過程中,過點![]() 作
作![]() 的切線交折線
的切線交折線![]() 于點
于點![]() ,將線段
,將線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到
得到![]() ,過
,過![]() 作
作![]() 于
于![]() .
.
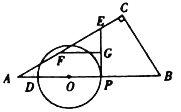
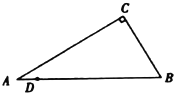

①當線段![]() 長度達到最大時,求
長度達到最大時,求![]() 的值;
的值;
②直接寫出點![]() 所經過的路徑長是________.(結果保留根號)
所經過的路徑長是________.(結果保留根號)
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)①
;(3)①![]() ;②
;②![]()
【解析】
(1)觀察圖中![]() 和
和![]() 的數量關系可得
的數量關系可得![]() ,而
,而![]() ,將
,將![]() 代入即可.
代入即可.
(2)![]() 與
與![]() 的一邊相切有兩種情況,先與
的一邊相切有兩種情況,先與![]() 相切,再與
相切,再與![]() 相切;兩種情況的解答方法都是連接圓心與切點,構造直角三角形,根據條件所給的特殊角的三角函數解答.
相切;兩種情況的解答方法都是連接圓心與切點,構造直角三角形,根據條件所給的特殊角的三角函數解答.
(3)①根據旋轉的性質可得![]() ,在
,在![]() 中根據三角函數可得
中根據三角函數可得![]() ,故當
,故當![]() 點與
點與![]() 點重合,
點重合,![]() 取得最大值時,
取得最大值時,![]() 有最大值,解之即可.
有最大值,解之即可.
②明顯以![]() 點與
點與![]() 點重合前后為節點,點
點重合前后為節點,點![]() 的運動軌跡分兩部分,第一部分為從
的運動軌跡分兩部分,第一部分為從![]() 開始運動到
開始運動到![]() 點與
點與![]() 點重合,即圖中的
點重合,即圖中的![]() ,根據
,根據![]() 求解;第二部分,根據
求解;第二部分,根據![]() 為定值可知其軌跡為圖中的
為定值可知其軌跡為圖中的![]() ,在
,在![]() 中用勾股定理求解即可.
中用勾股定理求解即可.
(1)![]() ,
,![]()
(2)情況1:與![]() 相切時,
相切時,
![]() 中,∵
中,∵![]()
∴![]()
∴![]() 解得
解得![]()
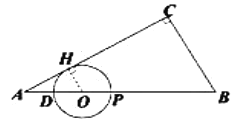
情況2:與![]() 相切時,
相切時,
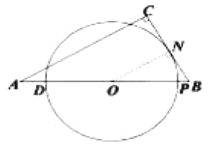
![]() 中,∵
中,∵![]()
∴![]() 即
即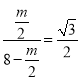
解得![]()
(3)①

在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴當![]() 最大時即
最大時即![]() 最大
最大
當點![]() 與點
與點![]() 重合時,
重合時,![]() 的值最大.
的值最大.
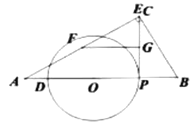
易知此時![]() .
.
在![]() 中,∵
中,∵![]() ∴
∴![]()
∴![]()
(3)![]() 軌跡如圖:從
軌跡如圖:從![]() 到
到![]() 到
到![]()
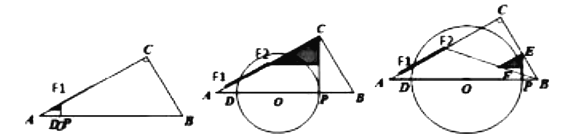
![]() ,
,
![]() ,
,
故![]() ,
,
![]() 到
到![]() 軌跡是線段理由如下:
軌跡是線段理由如下:
∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() 為定值,
為定值,
∴點![]() 的第二段的軌跡是線段
的第二段的軌跡是線段![]() .
.
在![]() 中,
中,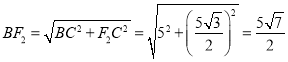 ,
,
所以點![]() 所經過的路徑長是
所經過的路徑長是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB、AC分別是⊙O的直徑和弦,點D為劣弧AC上一點,弦DE⊥AB分別交⊙O于E,交AB于H,交AC于F.P是ED延長線上一點且PC=PF.
(1) 求證:PC是⊙O的切線;
(2) 點D在劣弧AC什么位置時,才能使![]() ,為什么?
,為什么?
(3) 在(2)的條件下,若OH=1,AH=2,求弦AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】撫順某中學為了解八年級學生的體能狀況,從八年級學生中隨機抽取部分學生進行體能測試,測試結果分為A,B,C,D四個等級.請根據兩幅統計圖中的信息回答下列問題:
(1)本次抽樣調查共抽取了多少名學生?
(2)求測試結果為C等級的學生數,并補全條形圖;
(3)若該中學八年級共有700名學生,請你估計該中學八年級學生中體能測試結果為D等級的學生有多少名?
(4)若從體能為A等級的2名男生2名女生中隨機的抽取2名學生,做為該校培養運動員的重點對象,請用列表法或畫樹狀圖的方法求所抽取的兩人恰好都是男生的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
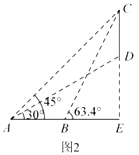
【題目】某數學興趣小組要測量實驗大樓部分樓體的高度(如圖1所示,![]() 部分),在起點
部分),在起點![]() 處測得大樓部分樓體
處測得大樓部分樓體![]() 的頂端
的頂端![]() 點的仰角為45°,底端
點的仰角為45°,底端![]() 點的仰角為30°,在同一剖面沿水平地面向前走16米到達
點的仰角為30°,在同一剖面沿水平地面向前走16米到達![]() 處,測得頂端
處,測得頂端![]() 的仰角為63.4°(如圖2所示),求大樓部分樓體
的仰角為63.4°(如圖2所示),求大樓部分樓體![]() 的高度約為多少米?(精確到1米)(參考數據:
的高度約為多少米?(精確到1米)(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖1中小黑點的個數記為![]() ,圖2中小黑點的個數記為
,圖2中小黑點的個數記為![]() ,圖3中小黑點的個數記為
,圖3中小黑點的個數記為![]() ,…
,…
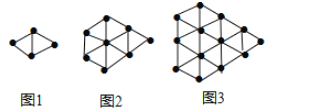
根據以上圖中的規律完成下列問題:
(1)圖4中小黑點的個數記為![]() ,則
,則![]() __________;
__________;
(2)圖![]() 中小黑點的個數記為
中小黑點的個數記為![]() ,則
,則![]() ___________(用含
___________(用含![]() 的式子表示);
的式子表示);
(3)若第![]() 個圖形中小黑點的個數比它前一個圖形中小黑點的個數多100,則
個圖形中小黑點的個數比它前一個圖形中小黑點的個數多100,則![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=2x+6與反比例函數![]() 的圖象交于點A(1,m),與x軸交于點B,平行于x軸的直線y=n(0<n<6)交反比例函數的圖象于點M,交AB于點N,連接BM.
的圖象交于點A(1,m),與x軸交于點B,平行于x軸的直線y=n(0<n<6)交反比例函數的圖象于點M,交AB于點N,連接BM.
(1)求m的值和反比例函數的表達式;
(2)觀察圖象,直接寫出當x>0時,不等式2x+6-![]() <0的解集;
<0的解集;
(3)當n為何值時,△BMN的面積最大?最大值是多少?
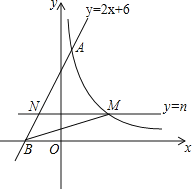
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,菱形OABC的邊長為2,點A在第一象限,點C在x軸正半軸上,∠AOC=60°,若將菱形OABC繞點O順時針旋轉75°,得到四邊形OA′B′C′,則點B的對應點B′的坐標為_____.
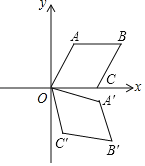
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與過點
,與過點![]() 平行于
平行于![]() 軸的直線相交于點
軸的直線相交于點![]() (點
(點![]() 在第一象限).拋物線的頂點
在第一象限).拋物線的頂點![]() 在直線
在直線![]() 上,對稱軸與
上,對稱軸與![]() 軸相交于點
軸相交于點![]() .平移拋物線,使其經過點
.平移拋物線,使其經過點![]() 、
、![]() ,則平移后的拋物線的解析式為__________.
,則平移后的拋物線的解析式為__________.
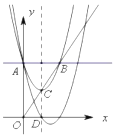
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com