
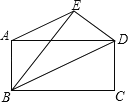
【題目】如圖,已知AB=3,BC=4,將矩形ABCD沿對角線BD折疊點C落在點E的位置,則AE的長度為( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
科目:初中數學 來源: 題型:
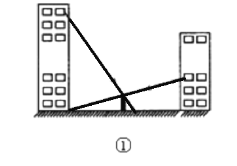
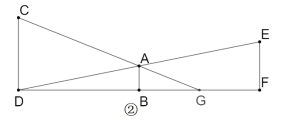
【題目】如圖,某中學兩座教學樓中間有個路燈,甲、乙兩個人分別在樓上觀察路燈頂端,視線所及如圖①所示.根據實際情況畫出平面圖形如圖②,CD⊥DF,AB⊥DF,EF⊥DF,甲從點C可以看到點G處,乙從點E恰巧可以看到點D處,點B是DF的中點,路燈AB高5.5米,DF=120米,BG=10.5米,求甲、乙兩人的觀測點到地面的距離的差.
查看答案和解析>>
科目:初中數學 來源: 題型:
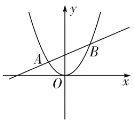
【題目】如圖,一次函數![]() 與拋物線
與拋物線![]() 交于A,B兩點,且點A的橫坐標是
交于A,B兩點,且點A的橫坐標是![]() ,點B的橫坐標是3,則以下結論:①拋物線
,點B的橫坐標是3,則以下結論:①拋物線![]() 的圖象的頂點一定是原點;②
的圖象的頂點一定是原點;②![]() 時,一次函數
時,一次函數![]() 與拋物線
與拋物線![]() 的函數值都隨x的增大而增大;③
的函數值都隨x的增大而增大;③![]() 的長度可以等于5;④當
的長度可以等于5;④當![]() 時,
時,![]() .其中正確的結論是( )
.其中正確的結論是( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
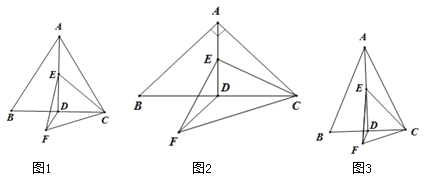
【題目】已知,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊中點,連接
邊中點,連接![]() ,點
,點![]() 為
為![]() 的中點,線段
的中點,線段![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() ,
,![]() .
.
(1)如圖1,當![]() 時,請直接寫出
時,請直接寫出![]() 的值;
的值;
(2)如圖2,當![]() 時,(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請寫出正確的結論,并說明理由;
時,(1)中的結論是否仍然成立?若成立,請給出證明;若不成立,請寫出正確的結論,并說明理由;
(3)如圖3,當![]() 時,請直接寫出
時,請直接寫出![]() 的值(用含
的值(用含![]() 的三角函數表示).
的三角函數表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系的坐標軸上按如下規律取點:![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() 在
在![]() 軸負半軸上,
軸負半軸上,![]() 在
在![]() 軸正半軸上,......,且
軸正半軸上,......,且![]()
![]() ......,設
......,設![]() ......,有坐標分別為
......,有坐標分別為![]() ,
,![]() ......,
......,![]() .
.
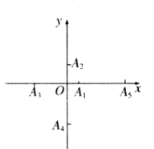
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)當![]() 時,直接寫出用含
時,直接寫出用含![]() 為正整數)的式子表示
為正整數)的式子表示![]() 軸負半軸上所取點.
軸負半軸上所取點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明投資銷售一種進價為每件20元的護眼臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數:y=﹣10x+500,在銷售過程中銷售單價不低于成本價,而每件的利潤不高于成本價的60%.
(1)設小明每月獲得利潤為w(元),求每月獲得利潤w(元)與銷售單價x(元)之間的函數關系式,并確定自變量x的取值范圍.
(2)當銷售單價定為多少元時,每月可獲得最大利潤?每月的最大利潤是多少?
(3)如果小明想要每月獲得的利潤不低于2000元,那么小明每月的成本最少需要多少元?(成本=進價×銷售量)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年4月15日傍晚法國地標性建筑巴黎圣母院突遭大火吞噬,導致屋頂和主尖塔坍塌,哥特式的玫瑰花窗損毀.為了重建巴黎圣母院,設計小組設計了一個由三色玻璃拼成的花窗,如圖所示,主體部分由矩形![]() 和半圓
和半圓![]() 組成,設半圓
組成,設半圓![]() 為區域
為區域![]() ,四個全等的直角三角形
,四個全等的直角三角形![]() 為區域
為區域![]() ,矩形內的陰影部分為區域
,矩形內的陰影部分為區域![]() ,其中
,其中![]() ,設
,設![]()
![]() 當
當![]() ,求區域
,求區域![]() 的面積.
的面積.
![]() 請用
請用![]() 的代數式表示出區域
的代數式表示出區域![]() 的面積并求出其最大值.
的面積并求出其最大值.
![]() 為了美觀,設置區域
為了美觀,設置區域![]() 與區域
與區域![]() 的面積之比為
的面積之比為![]() .區域
.區域![]() 、區域
、區域![]() 、區域
、區域![]() 分別鑲嵌紅、藍、黃色三種玻璃,已知這三種玻璃的單價之和為
分別鑲嵌紅、藍、黃色三種玻璃,已知這三種玻璃的單價之和為![]() 元(三種玻璃的單價均為整數),整個花窗鑲嵌玻璃共花費了
元(三種玻璃的單價均為整數),整個花窗鑲嵌玻璃共花費了![]() 元,求這三種玻璃的單價.(
元,求這三種玻璃的單價.(![]() 取
取![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】太陽能是來自太陽的輻射能量,對于地球上的人類來說,太陽能是對環境無任何污染的可再生能源,因此許多國家都在大力發展太陽能.如圖是2013﹣2017年我國光伏發電裝機容量統計圖.根據統計圖提供的信息,判斷下列說法不合理的是( )
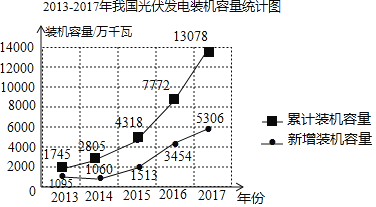
A.截至2017年底,我國光伏發電累計裝機容量為13078萬千瓦
B.2017年我國光伏發電新裝機容量占當年累計裝機容量的50%
C.2013﹣2017年,我國光伏發電新增裝機容量的平均值約為2500萬千瓦
D.2013﹣2017年,我國光伏發電新增裝機容量先減少后增加
查看答案和解析>>
科目:初中數學 來源: 題型:
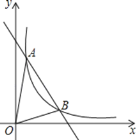
【題目】如圖,一次函數y=kx+b與反比例函數![]() 的圖象交于A(m,6),B(3,n)兩點.
的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)根據圖象直接寫出![]() 的x的取值范圍;
的x的取值范圍;
(3)求△AOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com